Teoria dos conjuntos
Saiba o que é a teoria dos conjuntos a partir de exemplos simples. Aprenda sobre tipos de conjuntos, relações entre eles, união, intersecção, diferença e diagrama de Venn.
A teoria dos conjuntos é uma parte da matemática que estuda conjuntos de diferentes tipos de elementos, como números, letras, nomes de pessoas, cidades, coisas em geral.
Os conjuntos são, geralmente, representados por letras maiúsculas do alfabeto e os elementos, que podem ser finitos ou infinitos, são escritos entre chaves { }.
Exemplos:
→ conjunto dos números ímpares menores que 10:
A = {1, 3, 5, 7, 9}
→ conjunto dos números múltiplos de 2:
B = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, …}
→ conjunto dos alunos que ficaram de recuperação em matemática (cada letra representa um aluno):
C = {a, b, c, d, e}
Agora, suponha que nenhum aluno ficou de recuperação, ou seja, o conjunto não tem nenhum elemento.
Quando não há elementos em um conjunto, o conjunto é chamado de conjunto vazio, sendo representado pelo símbolo .
Relação de pertinência – Pertence ou não pertence
Dado um conjunto, podemos indicar se um elemento pertence () ou não pertence (
) a esse conjunto.
Exemplo: A = {1, 2, 3, 4, 5, 6, 7}
O número 4 pertence ao conjunto A:
4 A
O número 9 não pertence ao conjunto A:
9 A
Relação de inclusão – Contido ou não contido
Quando temos dois ou mais conjuntos, podemos indicar se um conjunto está contido () ou não contido (
) em outro conjunto.
Um conjunto A está contido em um conjunto B quando todos os elementos de A pertencem a B.
Exemplo: A = {2, 4, 8}, B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} e C = {1, 3, 5, 7, 9, 11}
Todos os elementos de A pertencem a B, então A está contido em B:
A B
Nem todos os elementos de C pertencem a B, então C não está contido em B:
C B
Observações:
- O conjunto vazio (
) está contido em qualquer conjunto.
- Outra forma de representar a relação de pertinência é usando o símbolo de contém (
) ou não contém (
). Dizer que A está contido em B é o mesmo que dizer que B contém A.
No exemplo acima, podemos dizer que B contém A:
B A
Igualdade de conjuntos
Dois conjuntos, A e B, são iguais quando todos os elementos de A pertencem a B e todos os elementos de B pertencem a A.
Exemplo: A = {a, e, i, o, u}, B = {a, o, i, u, e} e C = {a, e, i, o, u, b}
Como todos os elementos de A pertencem a B e todos os elementos de B pertencem a A:
A = B
Todos os elementos de A pertencem a C, mas nem todos os elementos de C pertencem a A:
A C
Diagrama de Venn
O diagrama de Venn-Euler, também conhecido apenas por diagrama de Venn, é um gráfico para visualizar conjuntos, possibilitando entender melhor suas relações e propriedades.

União, intersecção e diferença entre conjuntos
A união, intersecção e diferença são conjuntos que podem ser formados a partir de dois conjuntos.
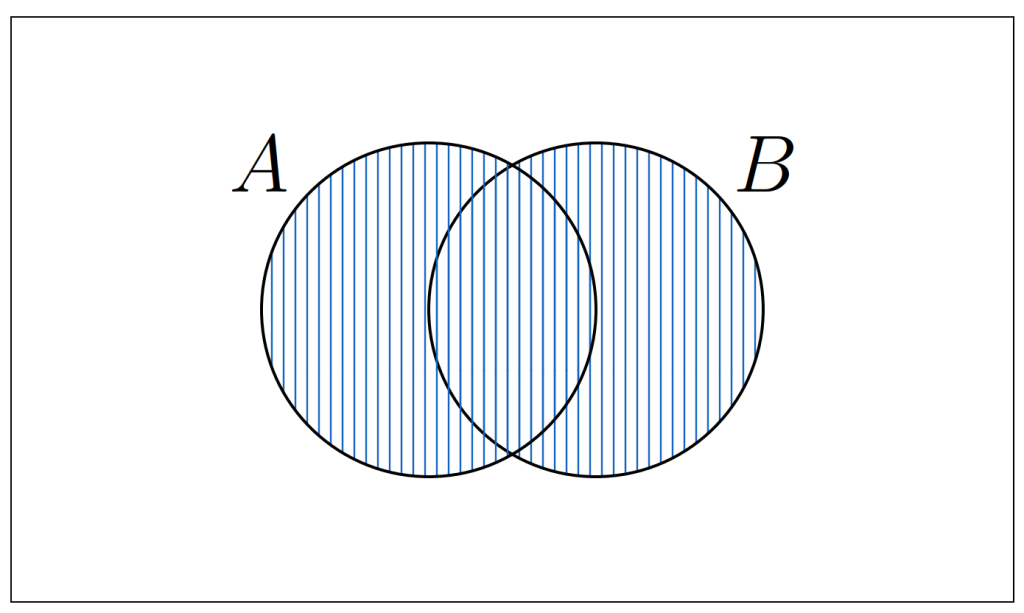
União de conjuntos
A união de conjuntos () corresponde ao conjunto formado por todos os elementos que estão em pelo menos um dos conjuntos.
Para expressar o conjunto união, basta considerar todos os elementos de A e todos os elementos de B, mas sem repetir os elementos que estão nos dois conjuntos.
Exemplo: A = {1, 2, 3, 4, 5, 6, 7} e B = {6, 7, 8, 9, 10}
A B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
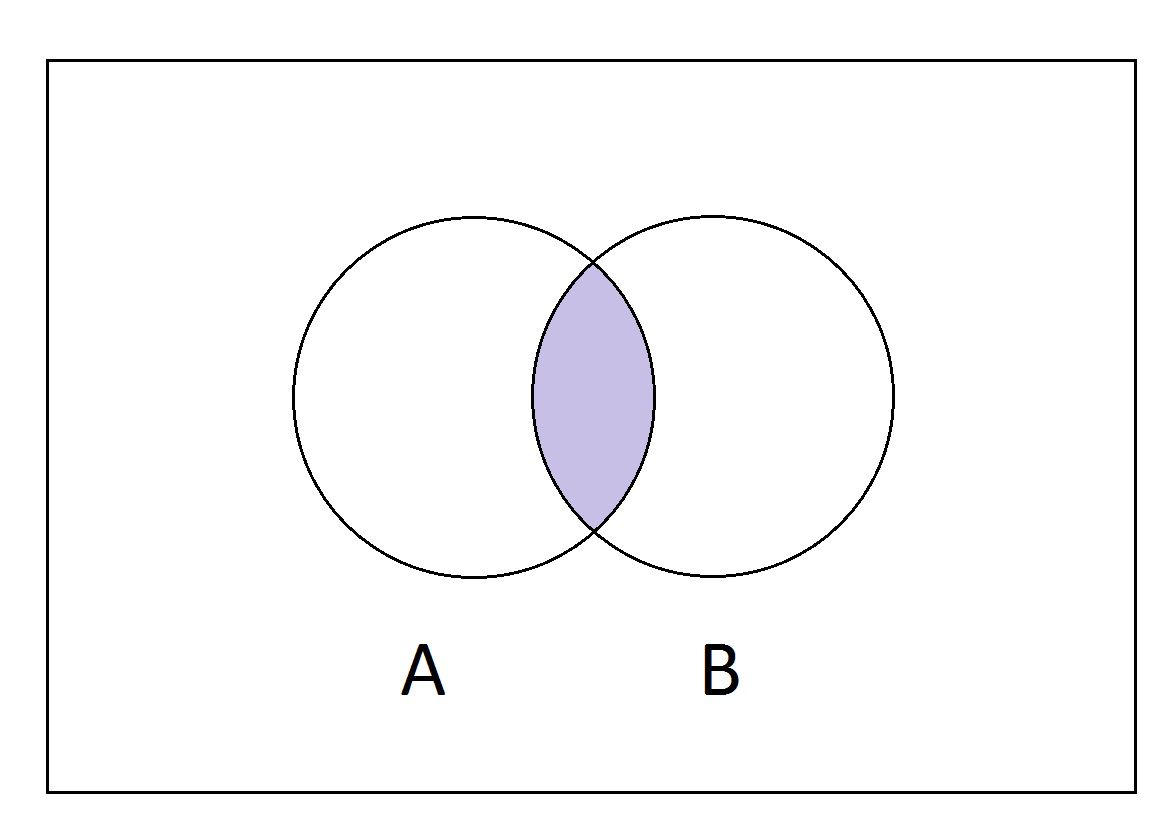
Intersecção de conjuntos
A intersecção de conjuntos () corresponde ao conjunto formado por todos os elementos que estão nos dois conjuntos.
Para expressar o conjunto intersecção, basta considerar todos os elementos que pertencem ao conjunto A e também pertencem ao conjunto B.
Exemplo: A = {1, 2, 3, 4, 5, 6, 7} e B = {6, 7, 8, 9, 10}
A B = {6, 7}
Diferença de conjuntos
A diferença de conjuntos corresponde ao conjunto formado por todos os elementos que estão no primeiro conjunto, mas que não estão no segundo conjunto.
Para expressar a diferença entre A – B, basta escrever o conjunto A sem os elementos que aparecem em B.
Exemplo: A = {1, 2, 3, 4, 5, 6, 7} e B = {6, 7, 8, 9, 10}
A – B = {1, 2, 3, 4, 5}
B – A = {8, 9, 10}
Você também pode se interessar:
- Conjuntos numéricos
- Probabilidade
- Lista de exercícios sobre conjuntos
- Lista de exercícios de conjunto dos números naturais


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.