Exercícios sobre coeficientes e concavidade da parábola
Saiba como determinar características importantes de uma parábola com uma lista de exercícios resolvidos sobre os coeficientes de uma função do 2° grau e a concavidade de uma parábola.
O gráfico de uma função do 2° grau, f(x) = ax² + bx + c, é uma parábola e os coeficientes a, b e c estão relacionados com características importantes da parábola, como a concavidade.
Além disso, as coordenadas do vértice de uma parábola são calculadas a partir de fórmulas que envolvem os coeficientes e o valor do discriminante delta.
Por sua vez, o discriminante também é uma função dos coeficientes e a partir dele podemos identificar se a função do 2° grau possui ou não raízes e quais são elas, quando existem.
Como você pode ver, a partir dos coeficientes podemos entender melhor a forma de uma parábola. Para entender mais, veja uma lista de exercícios resolvidos sobre a concavidade da parábola e os coeficientes da função do 2° grau.
Lista de exercícios sobre coeficientes e concavidade da parábola
Questão 1. Determine os coeficientes de cada uma das seguintes funções do 2° grau e diga qual a concavidade da parábola.
a)f(x) = 8x² – 4x + 1
b) f(x) = 2x² + 3x + 5
c) f(x) = 4x² – 5
e) f(x) = -5x²
f) f(x) = x² – 1
Questão 2. A partir dos coeficientes das funções quadráticas abaixo determine o ponto de intercepto das parábolas com o eixo das ordenadas:
a) f(x) = x² – 2x + 3
b) f(x) = -2x² + 5x
c) f(x) = -x² + 2
d) f(x) = 0,5x² + 3x – 1
Questão 3. Calcule o valor do discriminante e identifique se as parábolas interceptam o eixo das abscissas.
a) y = -3x² – 2x + 5
b) y = 8x² – 2x + 2
c) y = 4x² – 4x + 1
Questão 4. Determine a concavidade e o vértice de cada uma das parábolas a seguir:
a) y = x² + 2x + 1
b) y = x² – 1
c) y = -0,8x² -x + 1
Questão 5. Determine a concavidade da parábola, o vértice, os pontos de intercepto com os eixos e faça o gráfico da seguinte função quadrática:
f(x) = 2x² – 4x + 2
Resolução da questão 1
a) f(x) = 8x² – 4x + 1
Coeficientes: a = 8, b = -4 e c = 1
Concavidade: para cima, pois a > 0.
b) f(x) = 2x² + 3x + 5
Coeficientes: a = 2, b = 3 e c = 5
Concavidade: para cima, pois a > 0.
c) f(x) = -4x² – 5
Coeficientes: a = -4, b = 0 e c = -5
Concavidade: para baixo, pois a < 0.
e) f(x) = -5x²
Coeficientes: a = -5, b = 0 e c = 0
Concavidade: para baixo, pois a < 0.
f) f(x) = x² – 1
Coeficientes: a = 1, b = 0 e c = -1
Concavidade: para cima, pois a > 0.
Resolução da questão 2
a) f(x) = x² – 2x + 3
Coeficientes: a= 1, b = -2 e c = 3
O ponto de intercepto com o eixo y é dado por f(0). Esse ponto corresponde exatamente ao coeficiente c da função quadrática.
Ponto de intercepto = c = 3
b) f(x) = -2x² + 5x
Coeficientes: a= -2, b = 5 e c = 0
Ponto de intercepto = c = 0
c) f(x) = -x² + 2
Coeficientes: a= -1, b = 0 e c = 2
Ponto de intercepto = c = 2
d) f(x) = 0,5x² + 3x – 1
Coeficientes: a= 0,5, b = 3 e c = -1
Ponto de intercepto = c = -1
Resolução da questão 3
a) y = -3x² – 2x + 5
Coeficientes: a = -3, b = -2 e c = 5
Discriminante:
Como o discriminante é um valor maior que 0, então, a parábola intercepta o eixo x em dois pontos diferentes.
b) y = 8x² – 2x + 2
Coeficientes: a = 8, b = -2 e c = 2
Discriminante:
Como o discriminante é um valor menor que 0, então, a parábola não intercepta o eixo x.
c) y = 4x² – 4x + 1
Coeficientes: a = 4, b = -4 e c = 1
Discriminante:
Como o discriminante é igual a 0, então, a parábola intercepta o eixo x em um único ponto.
Resolução da questão 4
a) y = x² + 2x + 1
Coeficientes: a= 1, b = 2 e c= 1
Concavidade: para cima, pois a > 0
Discriminante:
Vértice:
V(-1,0)
b)y = x² – 1
Coeficientes: a= 1, b = 0 e c= -1
Concavidade: para cima, pois a > 0
Discriminante:
Vértice:
V(0,-1)
c) y = -0,8x² -x + 1
Coeficientes: a= -0,8, b = -1 e c= 1
Concavidade: para baixo, pois a < 0
Discriminante:
Vértice:
V(-0,63; 1,31)
Resolução da questão 5
f(x) = 2x² – 4x + 2
Coeficientes: a = 2, b = -4 e c = 2
Concavidade: para cima, pois a > 0
Vértice:
V(1,0)
Intercepto com o eixo y:
c = 2 ⇒ ponto (0, 2)
Intercepto com o eixo x:
Como , então, a parábola intercepta o eixo x em um único ponto. Esse ponto corresponde as raízes (iguais) da equação 2x² – 4x + 2, que podem ser determinadas pela fórmula de Bhaskara:
Logo, a parábola intercepta o eixo x no ponto (1,0).
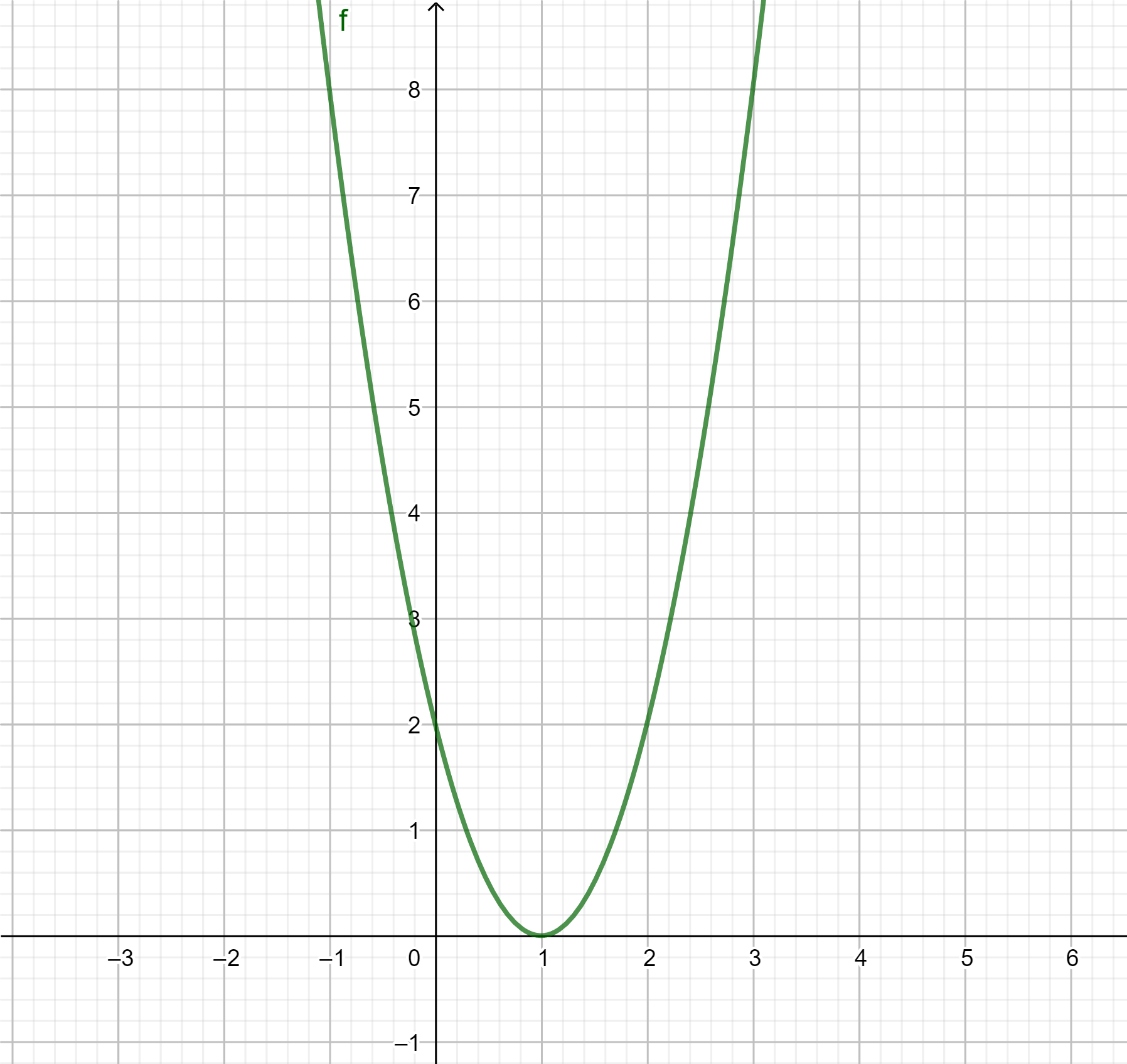
Gráfico:
Você também pode se interessar:
- Exercícios de função do primeiro grau (função afim)
- Funções trigonométricas – Seno, cosseno e tangente
- Domínio, contradomínio e imagem

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.