Poliedros – O que são, côncavos, convexos, de Platão, regulares
Os Poliedros são sólidos geométricos que contém todas as faces planas. Estas faces são nomeadas como polígonos. Saiba mais sobre essas formas.
Você já deve ter estudado as figuras geométricas espaciais, também conhecidas como sólidos geométricos. Estes podem ser divididos em poliedros e corpos redondos. Vamos conhecer agora um pouco sobre os poliedros.
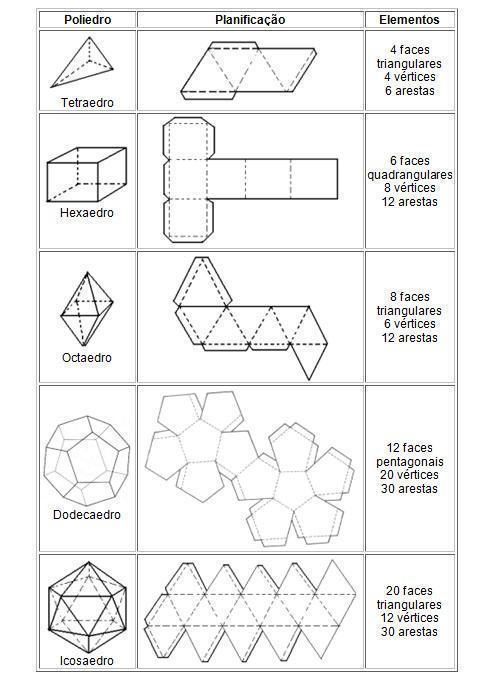
O poliedro possui faces, cada uma nomeada como polígono. Estas podem ser triângulos, quadriláteros, pentágono, entre outros.
Poliedro de Platão
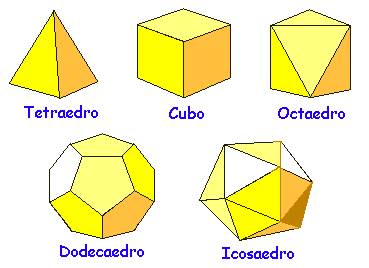
Platão estudou os chamados poliedros de Platão, que se encaixavam na nomeação de poliedros Regulares. Estes são: o cubo, o tetraedro, octaedro, dodecaedro e icosaedro.
Para ser considerado um poliedro de Platão, este deve conter as seguintes características:
- Todas as faces devem ser polígonos. Sendo regulares ou não;
- Todas as pontas devem conter o mesmo número de arestas;
- Os números de faces devem ser maior ou igual a 3.
Poliedros regulares
Para ser considerado um poliedro regular, este deve ser de Platão, quando seus polígonos ou faces são regulares e congruentes, além de ser convexo.
Um poliedro é considerado convexo quando qualquer segmento contido dentro da figura esteja totalmente dentro das arestas. Como por exemplo, um cubo. Confira agora cinco exemplos de poliedros regulares:
Poliedros côncavos
Os poliedros côncavos são os que possuem extremidades contidas fora da forma. Veja um exemplo de polígono côncavo:
Poliedros convexos
Os poliedros convexos, além de serem uma exigência para serem considerados regulares, são os que possuem todas as extremidades contidas dentro da forma. Veja um exemplo de poliedro convexo:
Relação de Euler
Vamos considerar que em um poliedro convexo V representa o número de vértices, F o número de faces e e A o número de arestas, podemos compor a seguinte fórmula:
V + F = A + 2
É importante entender que todos os poliedros convexos precisam auxiliar na fórmula. Os côncavos podem obedecer, mas não necessariamente.
Leia mais: Elementos de um poliedro

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.