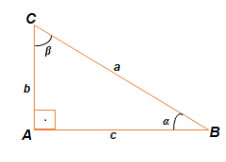
De acordo com a imagem acima, observamos que o Triângulo Retângulo é composto por três pontos. Pontos estes, no qual denomina-se ABC, reto em A com ângulos agudos medindo respectivamente α e β. Sendo b e c as medidas dos respectivos lados AB (Cateto) e AC (Cateto) e a, cujo lado corresponde a BC (Hipotenusa).
Propriedades
- Pode-se aplicar o Teorema de Pitágoras, dado ao triângulo ser retângulo: a²=b²+c²;
- Os ângulos internos de vértices C e B ao serem calculados, são respectivamente complementares, ou seja, α + β = 90°;
- Relativo ao ângulo de medida β, AB corresponde ao Cateto Oposto. Logo, AC corresponde ao Cateto Adjacente;
- Relativo ao ângulo de medida α, AC corresponde ao c;
- Cateto Oposto. Logo, AB corresponde ao Cateto Adjacente.
Definições
Seno
Sendo P uma imagem na circunferência trigonométrica e x um número real. Este é denominado como função:
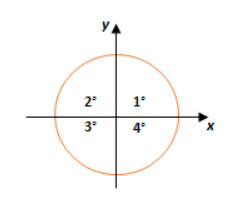
Seno tem a função periódica, onde seu período é 2π. O mesmo poderá ser positivo quando x pertencer ao 1° e 2°quadrantes, e negativo quando x pertencer ao 3° ou 4° quadrantes.
Razão, entre as medidas do Cateto Oposto com a Hipotenusa:
Cosseno
Sendo P uma imagem na circunferência trigonométrica e x um número real Este é denominado como função:
Cosseno possui a função periódica, onde seu período é 2π. A função será positiva quando x pertencer ao 1° e 4° quadrantes, e negativa quando x pertencer ao 2° e 3° quadrantes.
- No 1° e 2° quadrantes, a função de cosseno é decrescente e no 3° e 4° quadrantes, a função do cosseno é crescente.
Razão, entre as medidas do Cateto Adjacente com a Hipotenusa.
Tangente
Denominamos a função tangente como f: D = R, sendo
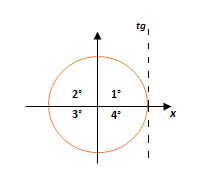
Dado x = x/2 + K. Sendo o K um número inteiro, o conjunto imagem f é R e sempre crescente. A Tangente possui sinal positivo quando a função está no 1° e 3° quadrantes e negativo no 3° e 4° quadrantes.
Razão entre as medidas do Cateto Oposto e Cateto Adjacente.
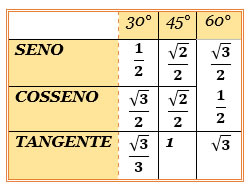
Tabela Trigonométrica dos ângulos notáveis
Tendo em vista um Triângulo Retângulo, as definições de Seno, Cosseno e Tangente permitem obter os seguintes ângulos de 30°, 45° e 60°. Estes, denominados como Valores, ou ângulos, Notáveis.

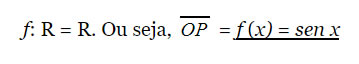


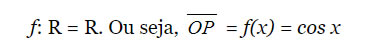
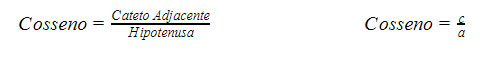
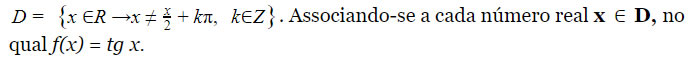
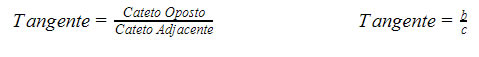
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.