A trigonometria é uma ferramenta utilizada para o cálculo de distâncias envolvendo o Triângulo Retângulo. Na antiguidade, os matemático utilizavam a mesma para cálculos realizados na astronomia para determinar a distância da Terra entre os demais Planetas.
A semelhança de triângulos:
Sendo os Triângulos polígonos, o estudo feito para identificar a semelhança entre eles é baseado nos correspondentes lados, sendo eles proporcionais e com ângulos correspondentemente congruentes (iguais).
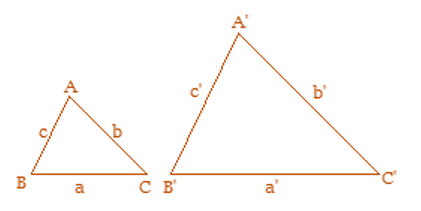
Os vértices A, B e C correspondem, respectivamente, aos vértices A’, B’ e C’. Sendo assim, deve-se montar as razões de proporcionalidade entre os lados correspondentes. Onde:
No caso de todos os lados correspondentes serem proporcionalmente iguais, o resultado das razões será igual a K.
Não obstante, a proporcionalidade entre os lados e vértices não é o suficiente para determinar a semelhança entre os triângulos. É necessário, também, que os ângulos sejam correspondentes. Assim:
Razões Trigonométricas:
Existem três Triângulos na Geometria, sendo eles denominados; Retângulo, Obtusângulo e Acutângulo. Hoje, estudaremos o Triângulo Retângulo e para isso, há algumas propriedades que você deve estar ciente.
- A soma de todos os ângulos devem ter 180°;
- Essa forma geométrica é conhecida por possuir um ângulo reto (90°), que sempre será oposto à hipotenusa;
- Os outros dois ângulos têm que possuir valores menores que 90°. Assim, são conhecidos como ângulos agudos.
*Antes de continuarmos devemos retomar que em um Triangulo Retângulo deve ser aplicado o Teorema de Pitágoras, onde:
h² = ca² + co²
h = Hipotenusa
ca = Cateto adjacente
co = Cateto oposto
Para identificarmos os Catetos e hipotenusa, é necessário observar que a hipotenusa é o lado oposto ao ângulo reto. Observe:
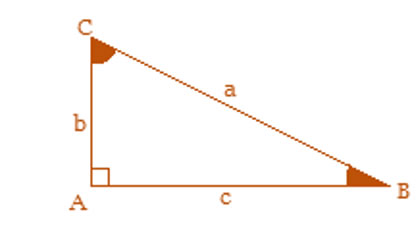
Hipotenusa – a
Catetos – c e b
Ângulo B:
Hipotenusa – b
Catetos – c e a
Ângulo C:
Hipotenusa – c
Catetos – b e a
Seno, Cosseno e Tangente:
Como podemos observar na figura abaixo.
- A Tangente de um ângulo no Triangulo retângulo é a razão entre o cateto Oposto e o Cateto Adjacente;
- O Seno de um ângulo no Triângulo Retângulo é a razão entre o Cateto Adjacente e a Hipotenusa;
- O Cosseno de um ângulo no Triangulo Retângulo é a razão entre o Cateto Adjacente e a Hipotenusa.
Exemplo:
Sendo sen α =1/2, determine o valor de x no triângulo retângulo.
A hipotenusa do triângulo é x. Sendo assim, o lado com medida conhecida é o Cateto Oposto ao ângulo α. Logo, temos que:

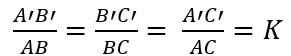
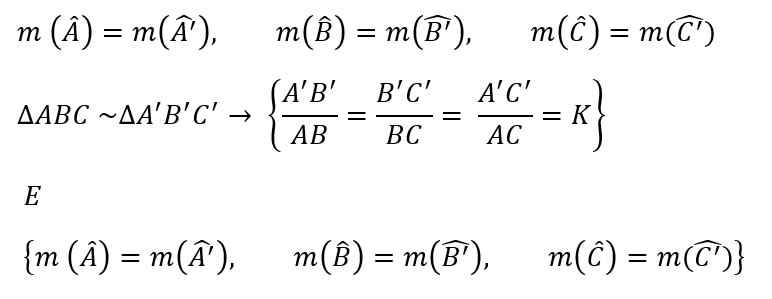


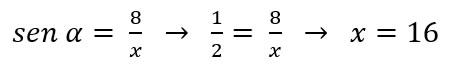
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.