Teorema de Tales

O Teorema de Tales estabelece uma relação entre as medidas de segmentos paralelos cortados por retas transversais.

O teorema é atribuído ao matemático e filósofo grego Tales de Mileto, que teria medido a altura de uma enorme pirâmide utilizando a sombra feita pelo Sol.

Para compreender o Teorema de Tales, é necessário entender alguns conceitos de razão e proporção entre segmentos de reta.

Razão entre dois segmentos

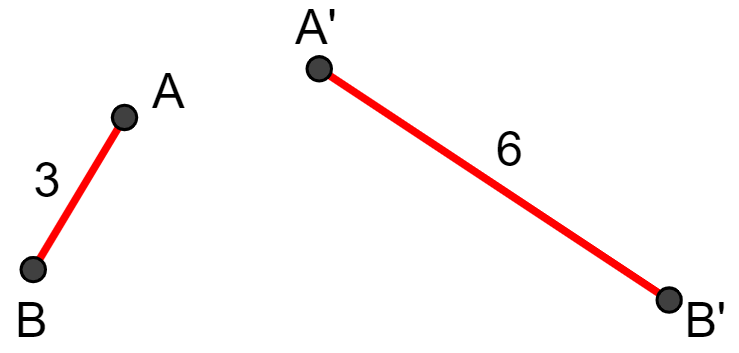
A razão entre dois segmentos é a divisão do comprimento de um segmento pelo comprimento do outro.

Exemplo:

A razão entre os segmentos  e  é dada por:

O que significa que o segmento  corresponde à metade do segmento  ou, de forma equivalente, que o segmento  corresponde ao dobro do segmento .

Segmentos proporcionais

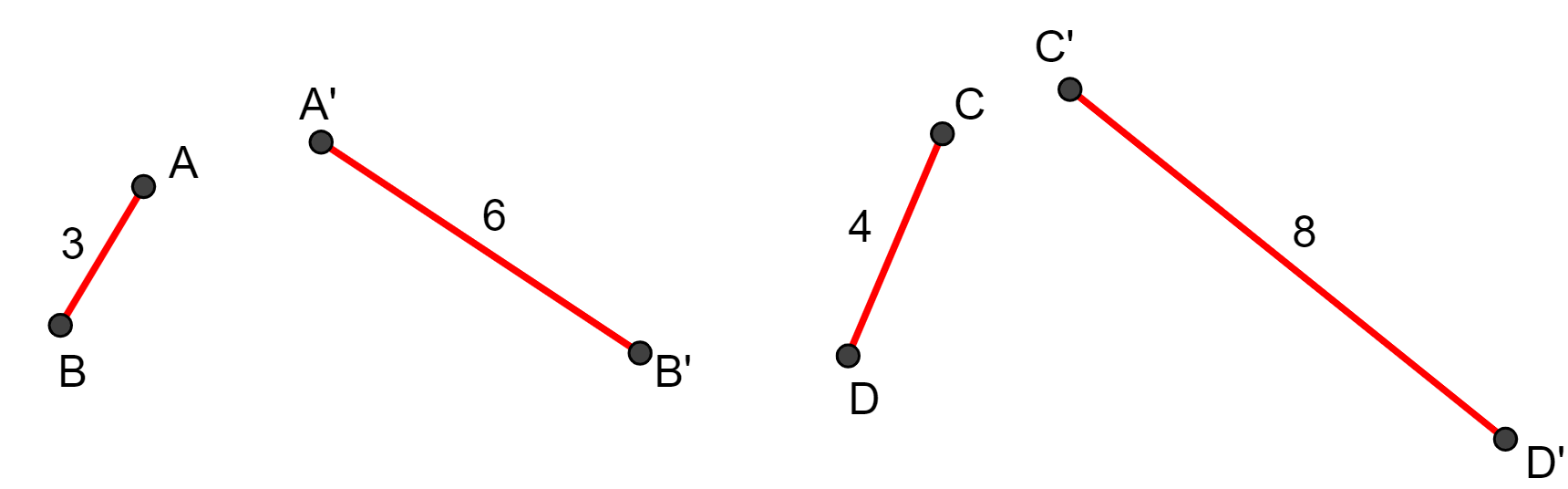
Dois pares de segmentos são proporcionais quando a razão entre os pares de segmentos é a mesma.

Exemplo:

Já vimos que a razão entre os segmentos  e  é 0,5. Agora, vamos calcular a razão entre os segmentos  e .

Embora os comprimentos sejam diferentes, a razão é a mesma, o segmento  corresponde a metade do segmento .

Assim, temos uma proporção:

Teorema de Tales

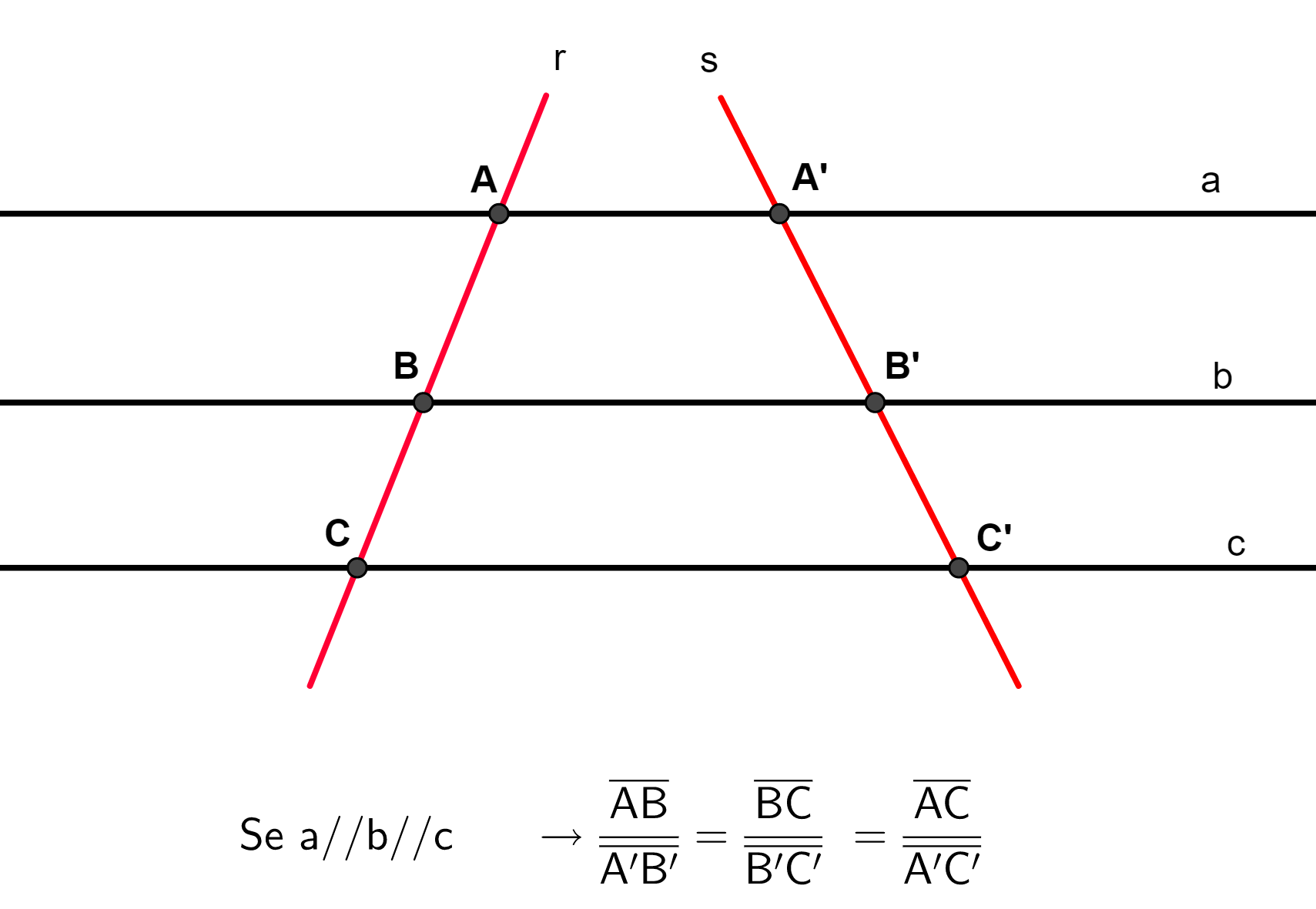
Considere três retas paralelas a, b e c, e duas retas transversais, r e s.

Pelo teorema de Tales, os segmentos da reta r são proporcionais aos segmentos da reta s.

Isso significa que, ao calcular a razão entre os segmentos, obtemos sempre um mesmo número.

Veja a representação:

O número obtido em cada razão é chamado de constante de proporcionalidade.

Você também pode se interessar:

• Lista de exercícios sobre teorema de Tales
• Lista de exercícios sobre semelhança de triângulos
• Congruência de triângulos