Como simplificar frações
As frações simplificadas facilitam muitos cálculos matemáticos. Aprenda o que você precisa para simplificar frações de um jeito muito prático e fácil.
Frações equivalentes nada mais são do que frações que representam a mesma quantidade ou parte de um todo.
Para entender como isso funciona, considere o seguinte exemplo:
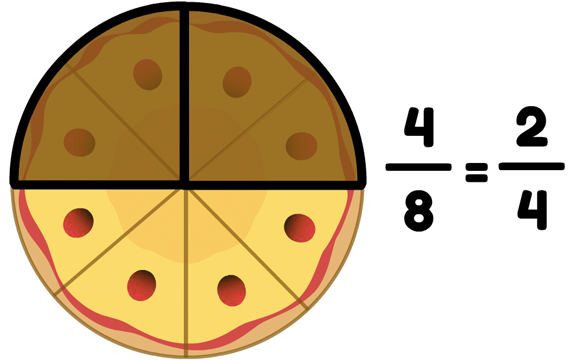
Em uma pizza de 8 pedaços, a fração que representa metade da pizza é . Contudo, se essa mesma pizza for dividida em apenas 4 pedaços, a metade dela é representada pela fração
. Veja na figura abaixo:
Apesar de terem numerador e denominador diferentes, as frações e
representam a mesma quantidade de pizza. Portanto, essas frações são equivalentes, o que significa que:
Pergunta 1: Será que existe uma fração equivalente a fração , com termos menores ainda?
Sim, a fração é equivalente a fração
, pois também representa a metade da pizza, quando ela é dividida em apenas dois pedaços.
Então, essas três frações são equivalentes:Pergunta 2: Será que existe uma fração equivalente a fração
, com termos menores ainda?
Não, esses são os menores valores possíveis, ou seja, já não conseguimos mais simplificar essa fração.
Nesse caso, dizemos que a fração é a forma irredutível da fração
.
O desenho da pizza facilitou encontrar frações equivalentes com termos menores para representar a metade da pizza.
Agora, vamos ver um modo prático e fácil de simplificar frações sem precisar do auxílio de uma imagem ilustrativa.
Como simplificar uma fração?
O primeiro número maior que 1 é o número 2. Os dois termos dessa fração são divisíveis por 2?
- 3 não é divisível por 2, pois o resto da divisão não é zero;
- 12 é divisível por 2, pois o resto da divisão é zero.
Os dois números devem ser divisíveis! Se os dois não são, vamos pro próximo número.
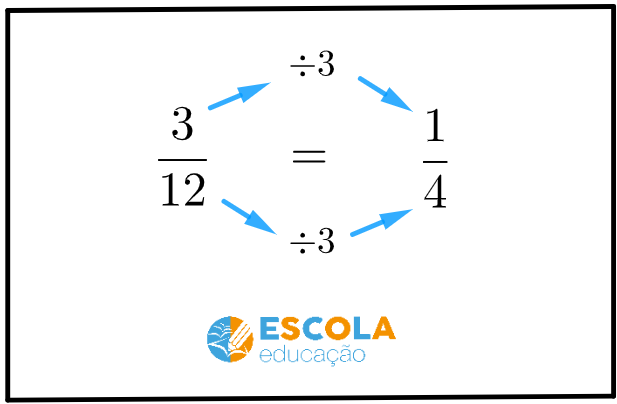
O próximo número é o 3. Os dois termos dessa fração são divisíveis por 3?
- 3 é divisível por 2, pois o resto da divisão é zero;
- 12 é divisível por 3, pois o resto da divisão é zero.
Então, para simplificar a fração, vamos dividir o numerador e o denominador por 3.
Daí, temos que .
Pergunta: É possível simplificar a fração ? Não, esses são os menores termos possíveis dessa fração.
Então, é a forma irredutível da fração
.
Leia também:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.