Como fazer adição e subtração de frações
Aprenda a somar e subtrair frações com o mesmo denominador e a calcular o mínimo múltiplo comum para frações com denominadores diferentes.
As frações são números usados para representar quantidades de um todo e assim como somamos ou subtraímos qualquer outro tipo de número, podemos somar ou subtrair números fracionários.
Na soma e subtração de frações, temos dois casos: quando os denominadores das frações são iguais e quando os denominadores das frações são diferentes.
Vamos ver como resolver cada um desses casos.
Somar ou subtrair frações com o mesmo denominador
Para somar ou subtrair frações que têm o mesmo denominador, basta somar ou subtrair os numeradores conforme a operação a ser feita e manter o denominador igual.
Exemplo 1: Calcular
- Numeradores: 5 e 2
- Operação a ser feita entre os numeradores:
- Denominador: 9
Então:
Exemplo 2: Calcular
- Numeradores: 5 e 2
- Operação a ser feita entre os numeradores:
- Denominador: 9
Então:
Exemplo 3: Calcular
- Numeradores: 1, 7 e 3
- Operação a ser feita entre os numeradores:
- Denominador: 10
Então:
Somar ou subtrair frações com denominadores diferentes
Para somar ou subtrair frações que possuem denominadores diferentes, antes, precisamos igualar esses denominadores para depois fazer a conta como já aprendemos.
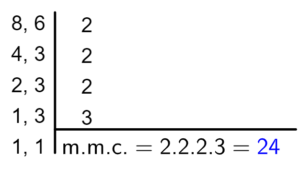
Exemplo: Calcular
Para igualar os denominadores, seguiremos cinco passos.
Passo 1) Calcular o mínimo múltiplo comum (m.m.c.) entre os denominadores das frações dadas.
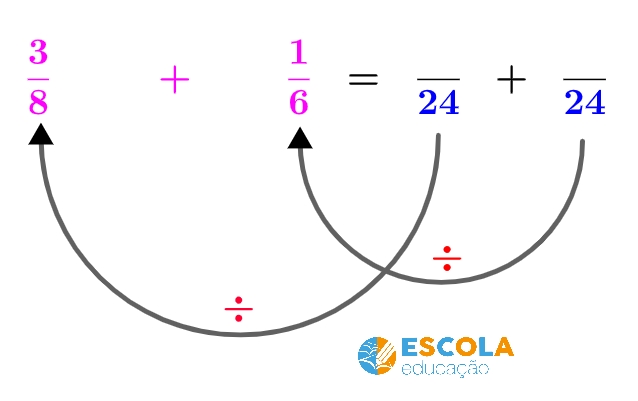
Passo 2) Escrever o m.m.c. como denominador de duas novas frações.
Passo 3) Dividir o m.m.c. por cada um dos denominadores das frações da conta que estamos fazendo (cor rosa).
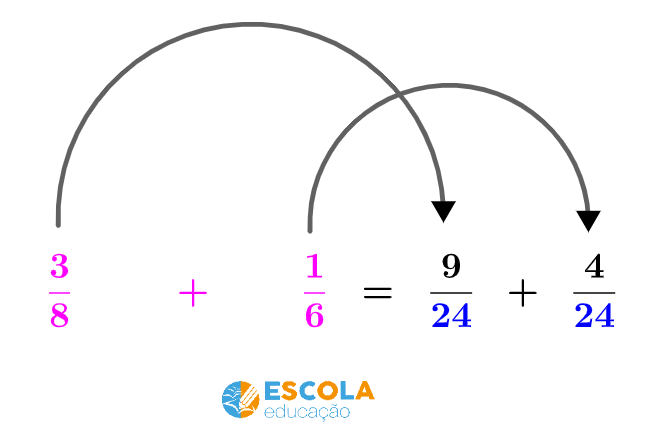
Passo 4) Multiplicar o resultado das divisões por cada um dos numeradores das frações da conta que estamos fazendo.
Passo 5) Escrever os resultados das multiplicações como numeradores das novas frações.
Finalizamos!
Agora já temos as frações com denominadores iguais: e para esse caso já vimos como calcular.
Então, .
Você também pode se interessar:


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.