Como conceito inicial, temos que as equações são expressões matemáticas que possuem incógnitas; coeficientes; sinais de igualdade e expoentes em sua composição. O grau de cada equação é determinado pelo maior expoente de uma das incógnitas. Assim temos que a equação do segundo grau é:
*O coeficiente a (ax²) não poderá ser igual à 0. Pois este se logo será 0x², anulando a si mesmo, o que se tornará uma Equação de 1° grau.
Exemplos:
3x² – 5x + 2 = 0
a = 3 b = 5 c = 2
2/4x + x² = 0
a = 1 b = 2/4x c* = 0
3x² – 9 = 0
a = 3x² b* = 0 c = 9
Raiz de uma equação do 2° grau
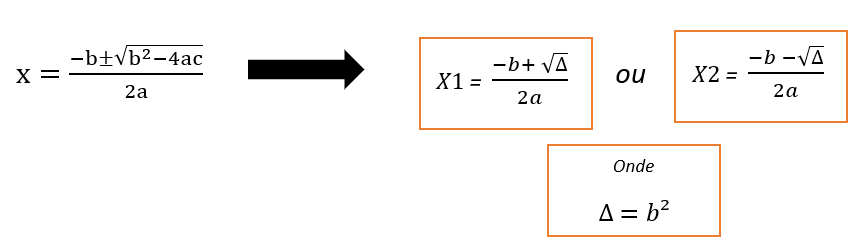
Esta equação possui no máximo duas raízes. Raízes estas, que podem ser determinadas através da seguinte fórmula, que é conhecida como fórmula de Bhaskara.
Discriminantes (∆)
Discriminante é o radical b² – 4ac, representado pela letra grega ∆ (delta). De acordo com o discriminante, temos três casos distintos a considerarmos, no qual:
- ∆ > 0 → A equação possui duas raízes reais e distintas.
- ∆ =0 → A equação possui duas raízes reais e iguais.
- ∆ <0 → A equação não possui raízes reais.
Exemplo:
Coeficientes e raízes
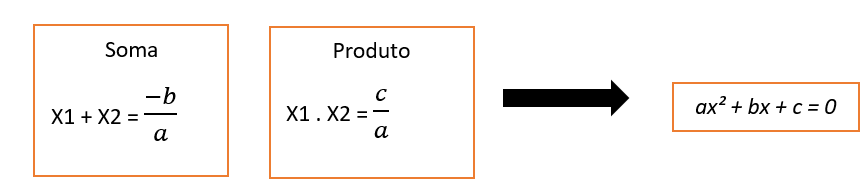
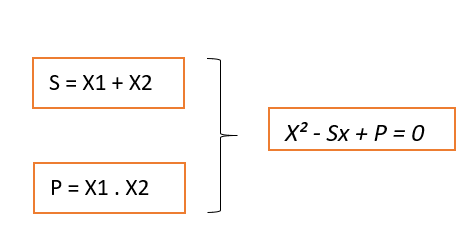
A equação de 2° grau possui duas relações entre as raízes X1 e X2 e os coeficientes a, b e c. relações estas, conhecidas como Soma e Produto, ou também, relações de Girard.
Exemplo:
X² + 3x – 10 = 0 (a = 1 b = 3 c = -10)
Determinação da Equação de 2° grau
Se X1 e X2 são as raízes de uma equação de 2° grau, então a mesma também pode ser escrita como:



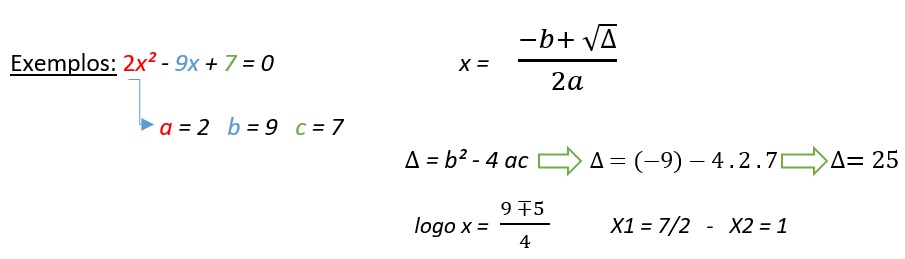

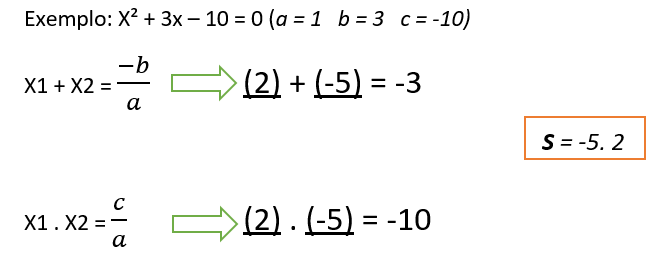
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.