Números decimais
Entenda o que são os números decimais, como eles são lidos e como fazer operações de soma, subtração, multiplicação e divisão entre eles.
Por exemplo, temos que , em que 1,47 é um número decimal, com parte inteira igual a 1 e parte decimal igual a 47.
Unidade decimal
As frações que têm numeradores iguais a 1 e denominadores 10, 100, 1000, … são chamadas de unidade decimal. Elas podem ser de 1ª, 2ª, 3ª,…, ordem.
Unidade decimal de 1ª ordem
Unidade decimal de 2ª ordem
Unidade decimal de 3ª ordem
Números racionais na forma decimal
Para escrever um número racional qualquer na forma decimal, só temos que escrever o número do numerador e colocar uma vírgula nele deixando:
- Uma casa após a vírgula, se o denominador da fração é 10;
- Duas casas após a vírgula, se o denominador da fração é 100;
- Três casas após a vírgula, se o denominador da fração é 1000;
E assim por diante.
Exemplos:
→ Uma casa após a vírgula pois o denominador é 10.
→ Uma casa após a vírgula pois o denominador é 10.
→ Uma casa após a vírgula pois o denominador é 10.
→ Duas casas após a vírgula pois o denominador é 100.
→ Três casas a mais após a vírgula pois o denominador é 1000. Acrescentamos zeros quando não há números sufientes para deixar após a vírgula.
Leitura de números decimais
Para leitura dos números decimais chamamos o primeiro número após a vírgula de décimo, o segundo número após a vírgula de centésimo, o terceiro número após a vírgula de milésimo, e assim por diante.
Exemplos:
0,1 → Um décimo
0,01 → Um centésimo
0,001 → Um milésimo
0,5 → Cinco décimos
0,5 → Cinco centésimos
0,005 → Cinco milésimos
0,25 → Vinte e cinco centésimos
0,418 → Quatrocentos e dezoito milésimos
1,7 → Um inteiro e sete décimos
1,72 → Um inteiro e setenta e dois centésimos
1,726 → Um inteiro e setecentos e vinte e seis milésimos
27,9 → Vinte e sete inteiros e nove décimos
254, 03 → Duzentos e cinquenta e quatro inteiros e três centésimos
Representação geométrica
Assim como as frações, os números decimais representam partes de um todo. Vamos ver como isso funciona geometricamente.
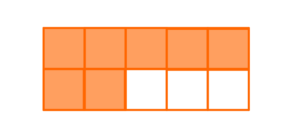
→ Um décimo corresponde a uma parte de um todo que está dividido em 10 partes iguais.
→ Sete décimos corresponde a sete partes de um todo que está dividido em 10 partes iguais.
→ Um inteiro e sete décimos corresponde a um todo mais sete partes de um todo que está dividido em 10 partes iguais.
Operações com números decimais
Adição e subtração
Para somar ou subtrair números decimais, basta colocarmos parte inteira embaixo de parte inteira, vírgula embaixo de vírgula, décimo embaixo de décimo, centésimo embaixo de centésimo, e assim por diante. Depois, fazemos a conta normalmente.
Exemplo 1: Calcular
Exemplo 2: Calcular
Para facilitar, acrescentamos zeros para que os números tenham a mesma quantidade de casas decimais após a vírgula.
Exemplo 3: Calcular
Multiplicação
Para multiplicar números decimais, basta realizar a conta como se não houvesse a vírgula e depois acrescentar uma vírgula no resultado final, de acordo com a soma do número de casas decimais nos fatores da multiplicação.
Exemplo: Calcular
Divisão
Na divisão, vamos multiplicar por 10, por 100, por 1000,…, de forma que a vírgula fique a direita do número, assim podemos “escondê-la”. A conta que teremos que fazer depois disso, é uma conta de divisão entre números inteiros.
Exemplo: Calcular
Assim, .
Leia também:
- Multiplicação (Matemática) – Contas, exemplos, tabuada, atividades
- Multiplicação de números decimais – Aprenda a multiplicar números com vírgula


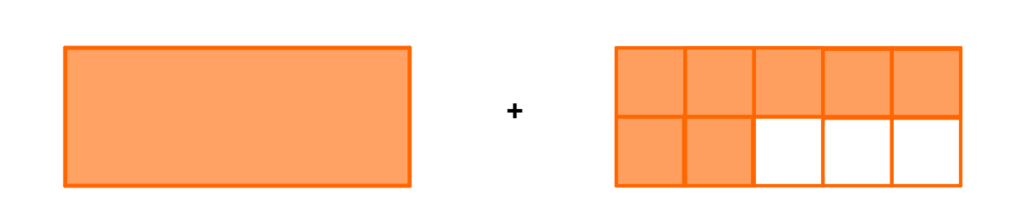
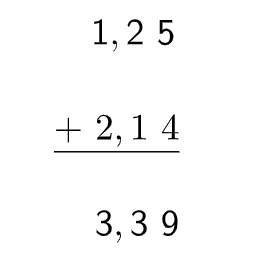
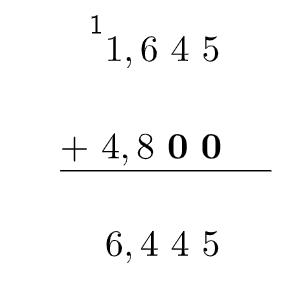
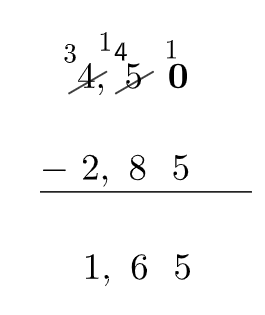
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.