Exemplo:
Racionais Positivos:
Quocientes de dois números inteiros com sinais iguais.
Racionais Negativos:
Quocientes de dois números inteiros com sinais desiguais.
Racionais não nulos (Q*):
Representado pelo acréscimo do (*) ao lado da letra. Este, é composto dos números racionais sem o zero (0).
Racionais não positivos (Q-):
Representado pelo acréscimo do sinal (-) ao lado da letra Q, este conjunto é composto dos números racionais negativos e o zero.
Racionais não negativos (Q+):
Representado pelo acréscimo do sinal (+) ao lado da letra Q, esse conjunto é composto dos números racionais positivos e o zero.
Contexto:
Os números naturais (N), são todos os números positivos.
Onde, N = {0, 1, 2, 3, 4, 5, 6, 7…}
Os números inteiros (Z), são um conjunto formado pelos elementos de números Naturais, e negativos.
Onde, Z = {… -4, -3, -2, -1, 0, 1, 2, 3, 4…}
Escrita Fracionária de Números Racionais:
- Sabendo que todo número é inteiro é racional, temo que: Todo número racional pode ser representado na forma facionária.
- 0.05 é um decimal exato, que pode ser representado pela fração 5100, pois é o resultado da divisão entre 5 e 100.
- 0,3333…é uma dízima periódica. Esta, por ser resultado da divisão entre dois números inteiros (1 e 3) pode ser representada por 13
- 79 É a representação do resultado da divisão entre 7 e 9, este formará a dízima periódica 0,7777…
- -43 e 12 (números inteiros), que podem ser escritos como,-431 e 12 (121)
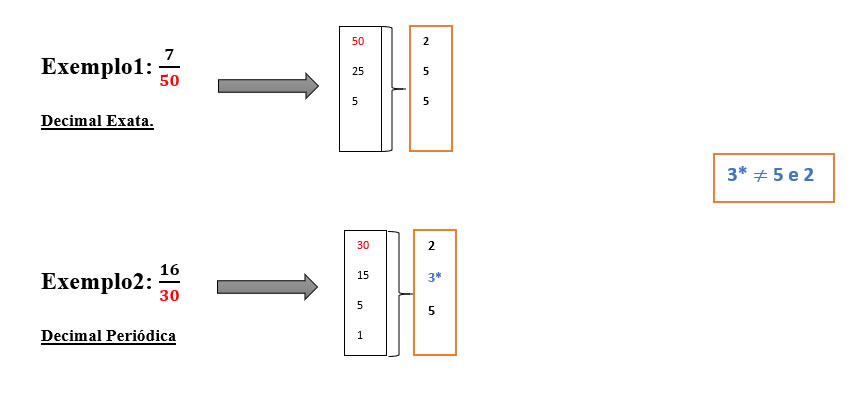
Mas como saber se uma determinada fração (sendo esta, irredutível), equivale a um decimal exato ou numa dízima periódica?
Para isso, é necessário que você decomponha o dominador. Ou seja, no caso de o dominador possuir fatores de 2 ou 5, o resultado será um decimal exato. No caso de o dominador ser fatores diferentes de 2 ou 5, então o resultado será uma dízima periódica.
Confira também:


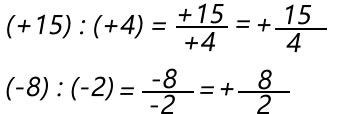
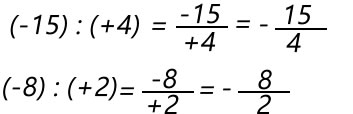

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.