Plano de aula – Polígonos regulares – 8º ano do Ensino Fundamental

Confira uma sugestão de plano de aula sobre propriedades dos polígonos regulares e construção dessas figuras geométricas, conforme as habilidades da BNCC.

Por Elainy Marciano Publicado em 17/09/2020 - 16:18

Os polígonos regulares possuem algumas propriedades importantes e, mais do que conhecer e utilizar fórmulas, é fundamental que os alunos possam compreender, de fato, o que significam tais propriedades.

Uma forma de propiciar isso aos estudantes, é a partir da construção das figuras geométricas. Dessa forma, os conceitos que antes pareciam abstratos e sem sentido, concretizam-se e se tornam naturais e simples de assimilar.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Pensando nisso, preparamos um plano de aula com base na habilidade EF08MA15 da BNCC, que diz respeito a construção de figuras geométricas a partir de instrumentos de desenho ou softwares de geometria.

Confira, a seguir, o plano de aula sobre polígonos regulares.

Plano de aula – Polígonos regulares

TEMA: Polígonos regulares e suas propriedades

HABILIDADES DA BNCC: (EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90°, 60°, 45° e 30° e polígonos regulares.

TEMPO SUGERIDO: 1 hora e 40 minutos

OBJETIVOS:

Conhecer as características e propriedades dos polígonos regulares;
Construir polígonos regulares utilizando transferidor, compasso e régua.

MATERIAL NECESSÁRIO:

Régua, transferidor e compasso (um de cada por aluno);
Quadro e giz ou pincel.

DESENVOLVIMENTO:

Para esta aula, é necessário que os alunos já tenham algum conhecimento sobre polígonos, nomenclatura, ângulos internos e externos.

1º momento

Inicie a aula retomando com os alunos o que são polígonos e quais, dentre os polígonos, são chamados de polígonos regulares.

Polígonos: figuras geométricas planas formadas por uma linha fechada simples (sem ponto de cruzamento) e cujos lados são apenas segmentos de reta (sem curvatura).
Polígonos regulares: são polígonos cujos lados são todos do mesmo tamanho e todos os ângulos internos têm a mesma medida.

Explique que, nessa aula, eles vão aprender sobre algumas características dos polígonos regulares.

Retome com eles a fórmula da soma dos ângulos internos ( $\dpi{120} S_i$ ) de um polígono convexo de $\dpi{120} n$ lados:

$\dpi{120} S_i=(n-2)\cdot 180^{\circ}$

E, também, lembre-os que a soma dos ângulos externos ( $\dpi{120} S_e$ ) de polígonos convexos é sempre igual a 360°, isto é:

$\dpi{120} S_e = 360^{\circ}$

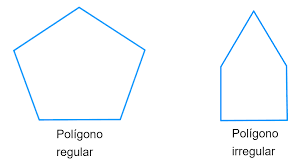
Desenhe, no quadro, um pentágono irregular e um pentágono regular. Peça que calculem $\dpi{120} S_i$ de cada um desses pentágonos.

Quando eles obterem a resposta ( $\dpi{120} S_i = 540^{\circ}$ ), pergunte se, a partir desse valor, eles podem inferir algo sobre cada um dos ângulos internos do polígono irregular? E do polígono regular?

Exponha no quadro, a seguinte questão:

Sabendo que a soma de todos os ângulos internos de qualquer pentágono é 540° e que todos os ângulos internos do pentágono regular têm a mesma medida, então, quanto mede cada ângulo?

Quando eles concluírem que basta dividir 540° por 5, apresente a fórmula para calcular a medida de cada ângulo interno de um polígono regular de $\dpi{120} n$ lados:

$\dpi{120} a_i = \frac{S_i}{n}= \frac{(n-2)\cdot 180^{\circ}}{n}$

Depois, apresente a mesma situação para os ângulos externos e a sua fórmula:

$\dpi{120} a_e=\frac{S_e}{n}=\frac{360^{\circ}}{n}$

Realize com eles algumas atividades sobre o uso dessas fórmulas. Peça que calculem a medida dos ângulos do hexágono regular, octógono regular, etc.

2º momento

Agora que os alunos já conhecem algumas das propriedades dos polígonos regulares, estão aptos a construir esse tipo de figura.

A ideia é utilizar régua, transferidor e compasso para construir diferentes tipos de polígonos regulares.

Comece com um polígono de poucos lados, como o pentágono regular. Mostre o passo a passo para a sua construção:

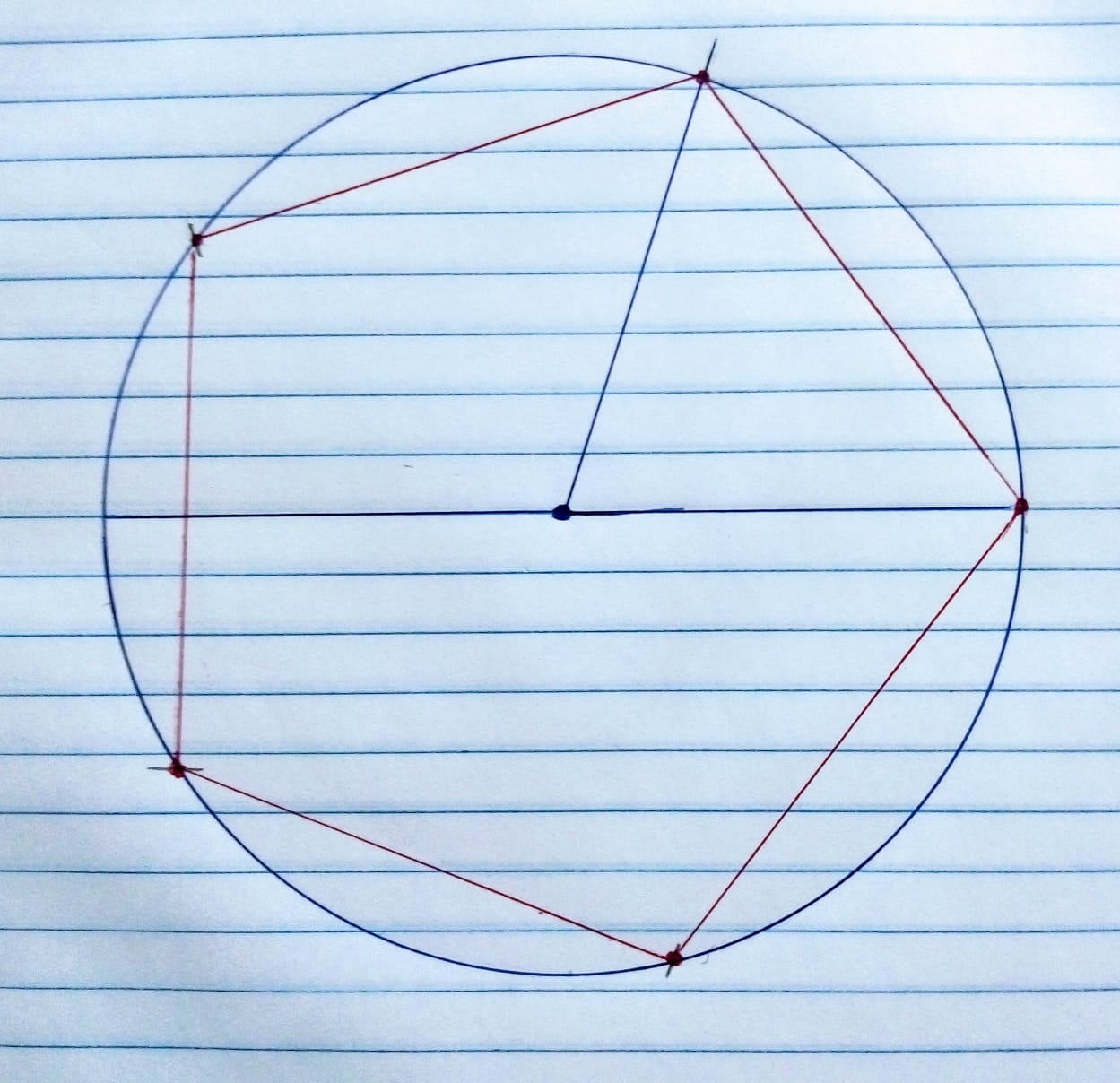
1) Com o transferidor, marque uma volta completa (360°) e faça um ponto no centro;

2) Com a régua, trace um segmento de reta que liga um ponto a outro do círculo, passando pelo centro;

3) Divida 360° pelo número de lados do polígono:

360° : 5 = 72°

4) Com o transferidor, marque um ângulo de 72°;

5) Marque o primeiro lado do polígono, ligando os dois pontos formados no círculo;

6) Com o compasso, faça uma abertura do tamanho do lado e marque os outros vértices do pentágono. Ligue os pontos com a régua, formando os outros lados.

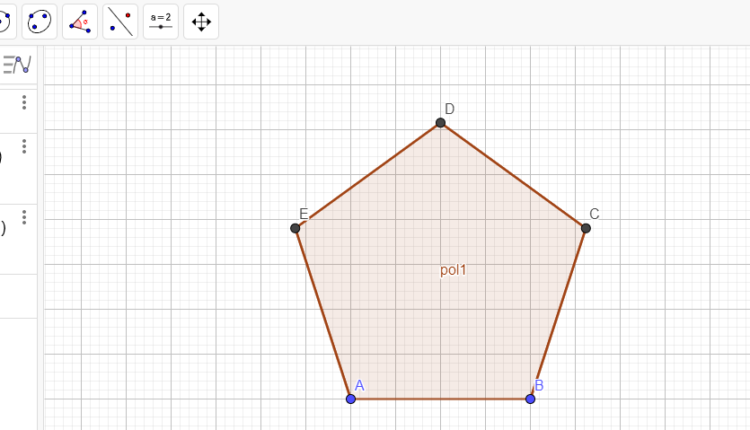
Caso tenha disponibilidade e recursos, como um laboratório de informática, outra ideia seria ensinar aos alunos como construir polígonos regulares no Geogebra, um software de geometria gratuito e bastante didático.

O Geogebra pode ser utilizado no próprio computador, fazendo o download no site. Assim como também há a opção de utilizar o programa online nesse mesmo site.

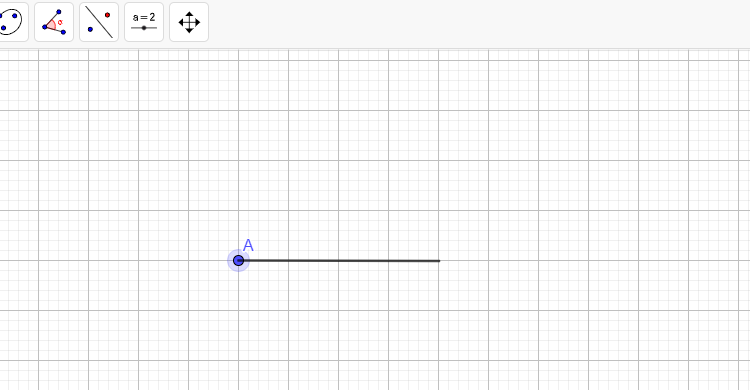
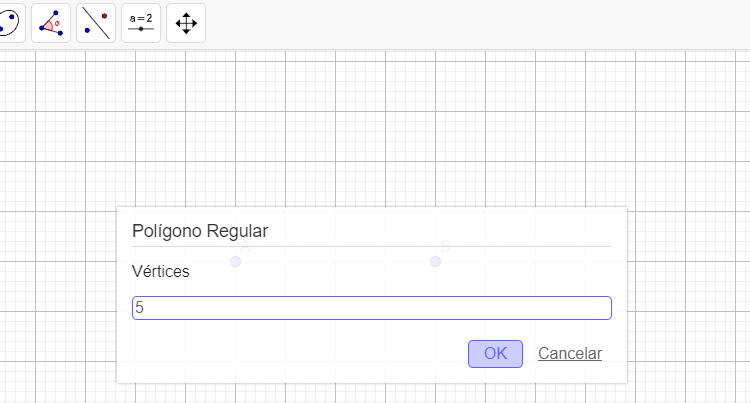
A construção de polígonos regulares no Geogebra é bem simples, basta que o usuário clique sobre a opção polígono regular, na aba de ferramentas, marque dois vértices do polígonos e digite o número de lados da figura no campo que irá aparecer no visor.

Prev 1 De 4 Next

AVALIAÇÃO:

A avaliação poderá ser feita a partir da observação do desempenho dos alunos durante as aulas. Além disso, faça perguntas como:

A partir da construção dos polígonos regulares, qual ou quais características importantes vocês observaram?
O que vocês podem dizer sobre os vértices dos polígonos regulares?

Você também pode propor, aos alunos, um desafio: construir um marcador de um relógio utilizando régua, compasso e transferidor.

A ideia é que eles reconheçam o marcador de um relógio como um dodecágono, já que as 12 horas são igualmente espaçadas.

Para baixar esse plano em PDF, clique aqui!

Você também pode se interessar:

Geometria plana Polígonos