Radiciação
Nesse post vamos te mostrar o que é a radiciação e quais são as principais propriedades dessa operação, que te ajudarão a resolver um monte de exercícios.
Assim, se na potenciação queremos descobrir o resultado da multiplicação repetida de um mesmo número, na radiciação queremos descobrir qual é esse número que multiplicamos repetidas vezes para chegar a tal resultado.
A operação de radiciação é formada pelos seguintes elementos:
Exemplos:
Significa que como 4 elevado ao quadrado é 16, então, a raiz quadrada de 16 é igual a 4.
Significa que uma vez que 2 elevado ao cubo é 8, então, a raiz cúbica de 8 é igual a 2.
Propriedades da radiciação
Vejamos abaixo as propriedades da radiciação e seus respectivos exemplos:
Propriedade 1) A raiz n-ésima de um número elevado a n é igual ao próprio número.
Exemplo: .
Propriedade 2) A raiz n-ésima de um número elevado a m é igual à raiz n-ésima do número elevado a m.
Exemplo: .
Propriedade 3) A raiz com índice n vezes p de um número elevado a m vezes p é igual a raiz n-ésima do número elevado a m.
Exemplo: .
Propriedade 4) A raiz com índice n dividido por p de um número elevado a m dividido por p é igual à raiz n-ésima do número elevado a m.
Exemplo: .
Propriedade 5) A raiz n-ésima do produto de dois números é igual ao produto das raízes n-ésimas dos números.
Exemplo: .
Propriedade 6) A raiz n-ésima da divisão de dois números é igual à divisão das raízes n-ésimas dos números.
Exemplo: .
Propriedade 7) A raiz m-ésima da raiz n-ésima de um número é igual à raiz com índice m vezes n desse número.
Exemplo: .
Você também pode se interessar:
- Matemática Básica – Encontrando a Raiz Quadrada
- Lista de exercícios de expressões numéricas
- Lista de exercícios de potenciação

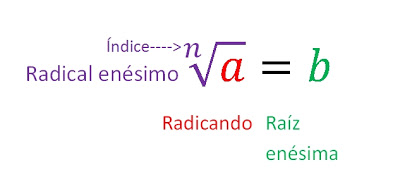
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.