Retas
Saiba o que são retas paralelas, concorrentes e coincidentes. Entenda, também, a diferença entre reta, semirreta e segmento de reta.
Na geometria, as retas são definidas como linhas infinitas, que não possuem espessura e nenhum tipo de curvatura.
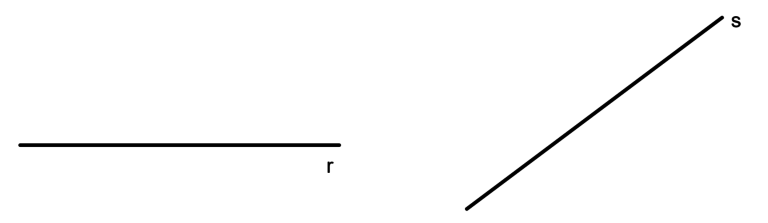
As retas são indicadas por letras minúsculas do alfabeto e representadas da seguinte forma:
Apesar dessa representação (finita), devemos imaginar a continuidade das retas para os dois lados, tendo em mente que elas não possuem um começo nem um fim.
Algumas características:
- Em uma reta, há infinitos pontos;
- Por um ponto no plano passam infinitas retas;
- Por dois pontos diferentes em um plano passa uma única reta;
- Uma reta pode ser vertical, horizontal ou inclinada.
Tipos de retas
Quando há duas retas, elas podem ser classificadas de acordo com as posições relativas entre elas.
Os principais tipos de retas são: retas paralelas, retas concorrentes ou retas coincidentes.
Retas paralelas
Duas retas que estão em um mesmo plano são chamadas de retas paralelas quando não possuem nenhum ponto em comum. São retas que nunca se cruzam.
As retas paralelas podem estar na horizontal, na vertical ou até mesmo inclinadas:
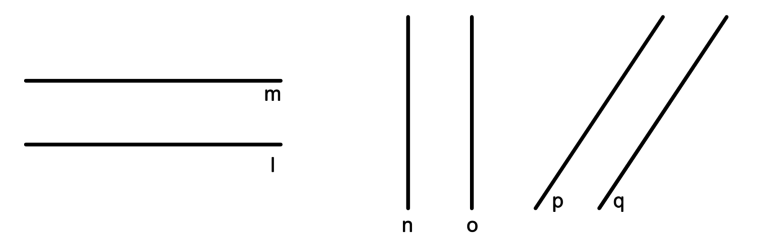
Retas concorrentes
Duas retas contidas em um mesmo plano são concorrentes ou secantes quando apresentam um único ponto em comum. São retas que se cruzam em algum momento.
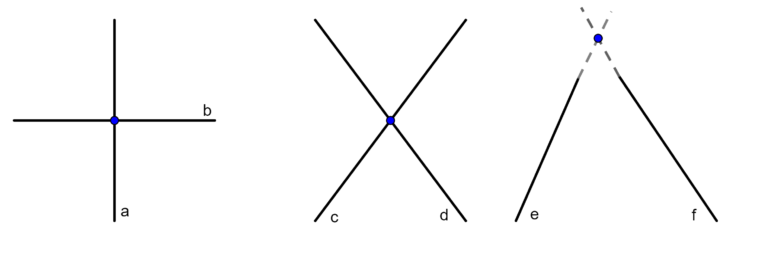
Retas coincidentes
Duas retas que ocupam a mesma posição em um plano são chamadas de retas coincidentes.
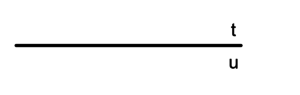
Semirreta e segmento de reta
Como já falamos, as retas são infinitas para os dois lados, elas não têm ponto de início nem de término.
Quando existe um ponto de início ou fim, ou os dois, temos “parte de uma reta”, que pode ser uma semirreta ou um segmento de reta.
Semirreta
Uma semirreta é uma parte de uma reta, ela possui um ponto de início (ou fim), sendo infinita apenas em um dos lados.
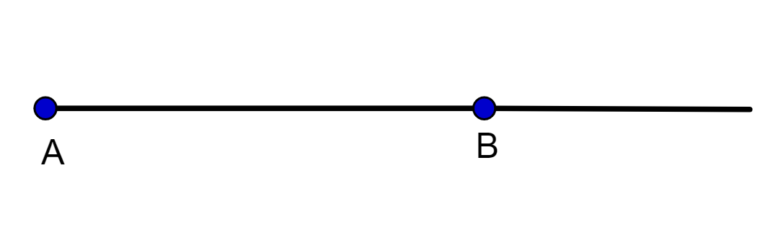
Observe que a semirreta do exemplo apenas passa pelo ponto B, ela não termina nele.
Segmento de reta
Um segmento de reta é uma parte de uma reta, ele possui ponto de início e fim.
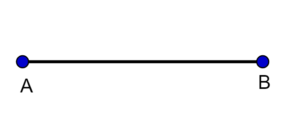
Os pontos A e B são chamados de extremidades do segmento.
Você também pode se interessar:
- Classificação dos triângulos
- Ângulos – Tipos, classificações e exemplos
- Ângulos complementares e suplementares

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.