Ângulos – Tipos, classificações e exemplos
Existem vários tipos de ângulos. Aprenda o que é ângulo agudo, ângulo reto, ângulo obtuso e ângulo raso. Veja também o que são ângulos congruentes, consecutivos, adjacentes, complementares e suplementares.
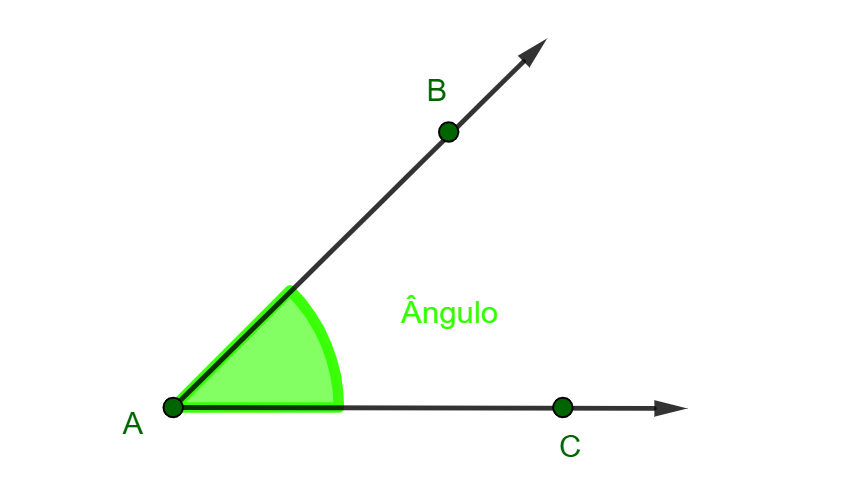
O que é ângulo? Ângulo é a região do plano formada por duas semirretas de mesma origem, ou seja, é a abertura entre duas semirretas que partem de um mesmo ponto. A medida de um ângulo é dada pela medida de sua abertura e é expressa em graus.
Existem vários tipos de ângulos e eles podem ser classificados individualmente, de acordo com sua medida, ou de dois em dois, de acordo com as medidas, a posição entre eles e a soma das suas medidas.
Ângulo agudo, ângulo reto, ângulo obtuso e ângulo raso
Ângulo agudo: É todo ângulo cuja medida é maior que 0º e menor que 90º, como por exemplo: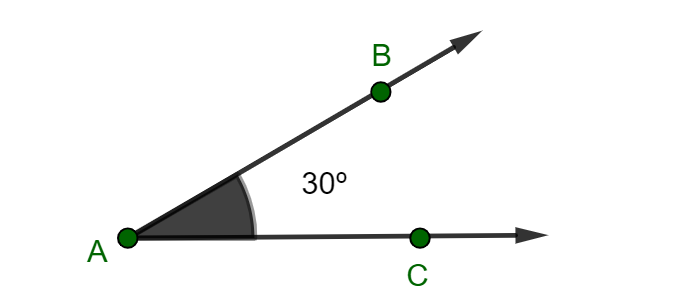
Ângulo Obtuso: É todo ângulo que mede mais que 90º e menos que 180º, por exemplo:
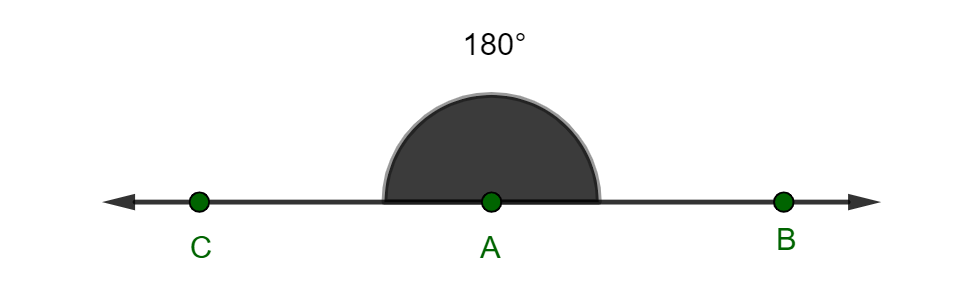
Ângulo raso ou de meia volta: É o ângulo cuja medida é igual a 180º:
Podemos ter, ainda, o ângulo nulo, que mede 0º, e o ângulo de uma volta, com medida igual a 360º.
Ângulos congruentes
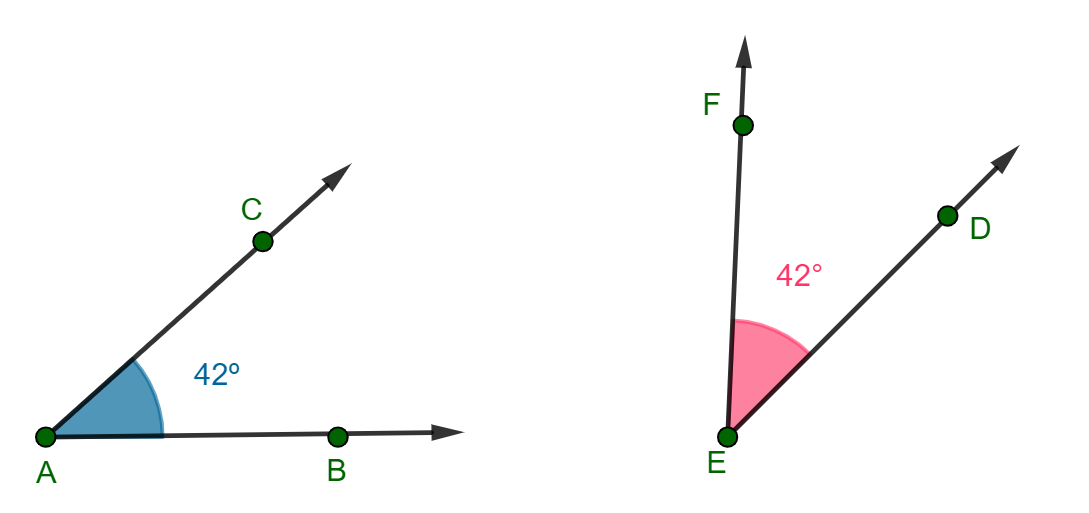
Dois ângulos são congruentes quando eles têm a mesma medida. Por exemplo, os ângulos e
a seguir:
Ângulos consecutivos e ângulos adjacentes
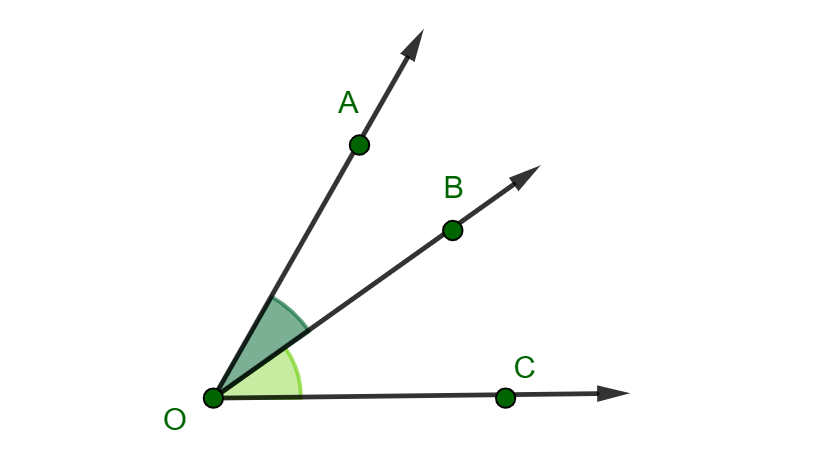
Ângulos consecutivos: São dois ângulos que possuem o mesmo vértice e têm um lado em comum. Na imagem abaixo, por exemplo, temos que:
e
são consecutivos com vértice no ponto
e com lado
em comum;
e
são consecutivos com vértice no ponto
e com lado
em comum;
e
são consecutivos com vértice no ponto
e com lado
em comum.
Ângulos adjacentes: São ângulos consecutivos que não possuem pontos internos em comum. Assim, no exemplo anterior, os ângulos:
e
são ângulos adjacentes;
e
não são adjacentes;
e
não são adjacentes.
Se ainda ficou em dúvidas, desenhe esses ângulos em um papel e pinte a região correspondente aos ângulos
e
com cores diferentes cada uma.
Você verá que a região do ângulo
receberá as duas cores, pois essa região também faz parte do ângulo
, isto é, existem pontos em comum entre esses ângulos. Por isso esses dois ângulos não são adjacentes.
O mesmo não acontecerá com os ângulos
e
. Se você pintar cada um deles com cores diferentes, não haverá nenhuma parte do desenho colorida duas vezes, ou seja, eles não possuem pontos em comum. Por isso são adjacentes.
Ângulos complementares e ângulos suplementares
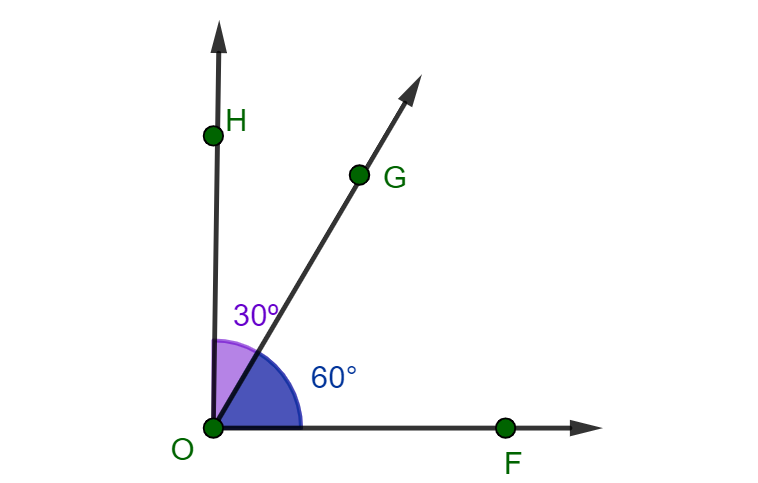
Ângulos complementares: Dois ângulos são complementares quando a soma de suas medidas é igual a 90º. Por exemplo:
Os ângulos e
acima são complementares, pois a soma das suas medidas é 30º + 60º = 90º.
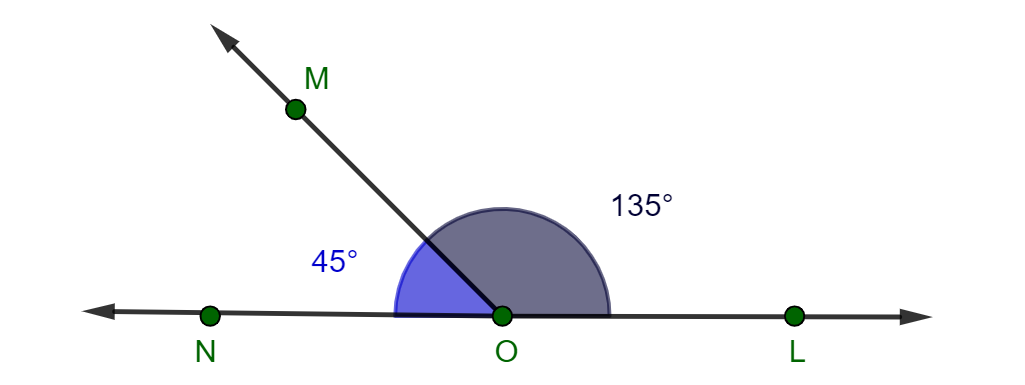
Ângulos suplementares: Dois ângulos são suplementares quando a soma de suas medidas é igual a 180º, por exemplo:
A soma das medidas dos ângulos e
é 135º + 45º = 180º. Por isso, esses dois ângulos são suplementares.
Você também pode se interessar:
- Ângulos complementares e suplementares
- Trigonometria no Triângulo Retângulo
- Área do Triângulo
- Regra de três – Veja os tipos e aprenda como calcular
- Monômios – O que são? Para que servem? Como fazer operações entre monômios?



Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.