Semelhança de triângulos

Semelhança de triângulos é uma propriedade que pode ou não haver entre dois triângulos. A semelhança está relacionada aos ângulos e lados dos triângulos.

Dois triângulos são semelhantes quando possuem os três ângulos correspondentes com medidas iguais e os três lados correspondentes proporcionais.

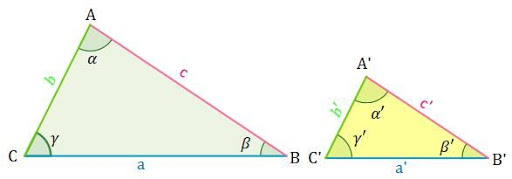
Para que os triângulos ABC e A’B’C’ da figura sejam semelhantes devemos ter:

,        ,          e     

Razão de proporcionalidade

A razão de proporcionalidade é o valor que obtemos quando calculamos a razão entre os lados correspondentes de triângulos semelhantes.

Exemplo:

Calculando a razão entre os lados correspondentes, obtemos sempre um mesmo valor:

Os lados correspondentes são proporcionais e a razão de proporcionalidade é igual a 1/2 ou 0,5.

Casos de semelhança de triângulos

Podemos identificar se dois triângulos são semelhantes através de três casos diferentes.

1º caso: Ângulo — Ângulo (AA)

2º caso: Lado — Lado — Lado (LLL)

3º caso: Lado — Ângulo — Lado (LAL)

Teorema Fundamental da Semelhança

O Teorema Fundamental da Semelhança nos diz que quando traçamos uma reta que intersecta dois lados de um triângulo em pontos diferentes e que é paralela ao terceiro lado do triângulo, obtemos outro triângulo que é semelhante ao anterior.

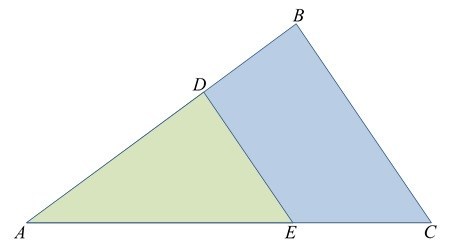
Por esse teorema, podemos dizer que os triângulos ABC e ADE da figura são semelhantes.

Você também pode se interessar: 

• Teorema de Tales
• Lista de exercícios sobre teorema de Tales
• Congruência de triângulos
• Lista de exercícios sobre semelhança de triângulos