Circunferência Trigonométrica
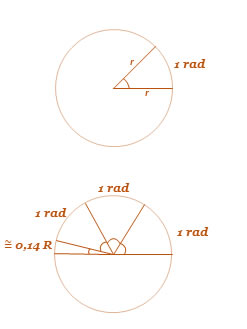
Radiano: Define-se como a medida de um aro cujo comprimento é igual ao raio da circunferência. Um radiano mede, aproximadamente 57,3°. Mas quantos radianos podemos ter, caso efetuarmos uma volta completa no círculo?
Sendo um total de 360° uma volta completa, podemos encontrar o comprimento de uma circunferência através da fórmula:
C = 2πR = 6,28R
Sendo o ângulo de 180° 1π, então este mede, aproximadamente 3,14R. Assim,
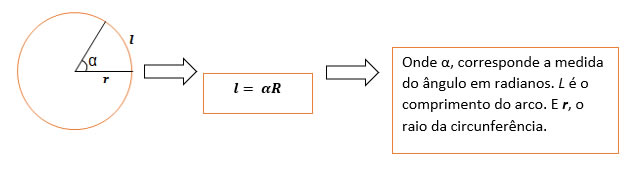
- O comprimento do arco de raio r pode ser determinado como:
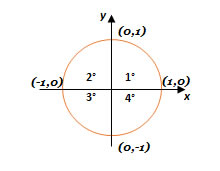
- A circunferência trigonométrica é uma representação gráfica que ajuda no cálculo das razões trigonométricas.
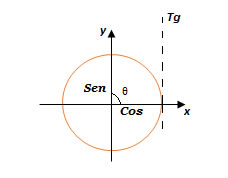
- Como está representado abaixo, o Seno corresponde ao eixo vertical (y). Logo, o Cosseno corresponde ao eixo horizontal (x).
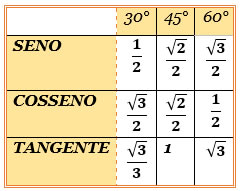
Ângulos Notáveis
Chamamos de ângulos notáveis, aqueles que mais se mostram no cálculo da trigonometria. Estes ângulos 30°, 45° e 60°; podem representar as razões trigonométricas de um ângulo qualquer da circunferência.
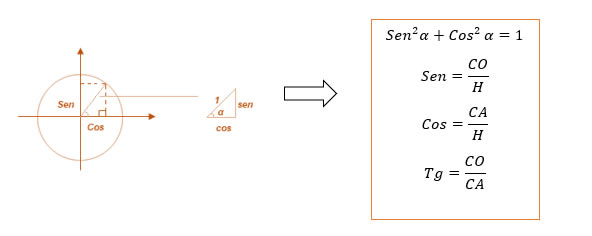
Relação fundamental da Trigonometria
Quaisquer triângulos
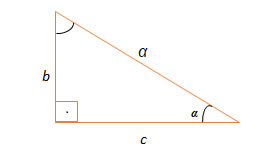
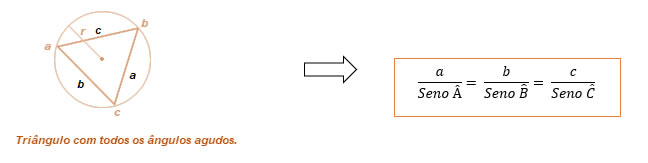
Lei dos Senos: A medida dos lados dos triângulos é diretamente proporcional aos Senos dos respectivos ângulos opostos. A constante é igual à medida do diâmetro da circunferência circunscrita de um triângulo qualquer (que não possui um ângulo de 90°). Assim, para um triângulo ABC de lados a, b e c, podemos representar como:
Lei dos Cossenos: Em qualquer triângulo, podemos calcular como o quadrado da medida de um dos lados, o resultado é igual à soma dos quadrados das medidas dos lados restantes, subtraída pelo dobro do produto da medida desses lados pelo Cosseno do ângulo formado por eles. Fórmula:
Podemos também, a partir da lei dos cossenos, obter as seguintes relações entre os lados e os ângulos de um triângulo.

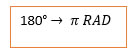


Necessário para colocar você esta pouco note finalmente muito obrigado again considerando o bonito dicas você compartilhado neste site . É assim extremamente generoso com pessoas como você para dar desimpedido exatamente o que um número de nós {poderiam ter | poderiam possivelmente ter | poderiam ter | teriam | vendido como um ebook para fazer alguns dólares para seu próprio fim , principalmente dado que you bem feito tried it no caso de você desejado . These princípios adicionalmente servido para fornecer uma maneira fácil de encontrar uma boa maneira de ter certeza de que outras pessoas on-line tem o mesmo fervor o mesmo que meu próprio para descobrir muito mais com referência a this condition . Eu tenho certeza existem milhões de mais agradáveis oportunidades no futuro para indivíduos que confira seu site