Ângulos opostos pelo vértice
Entenda o que são ângulos opostos pelo vértice e quais são suas propriedades.
São denominados ângulos opostos pelo vértice (o.p.v.) aqueles cujos lados de um são prolongamentos dos lados do outro e vice-versa.
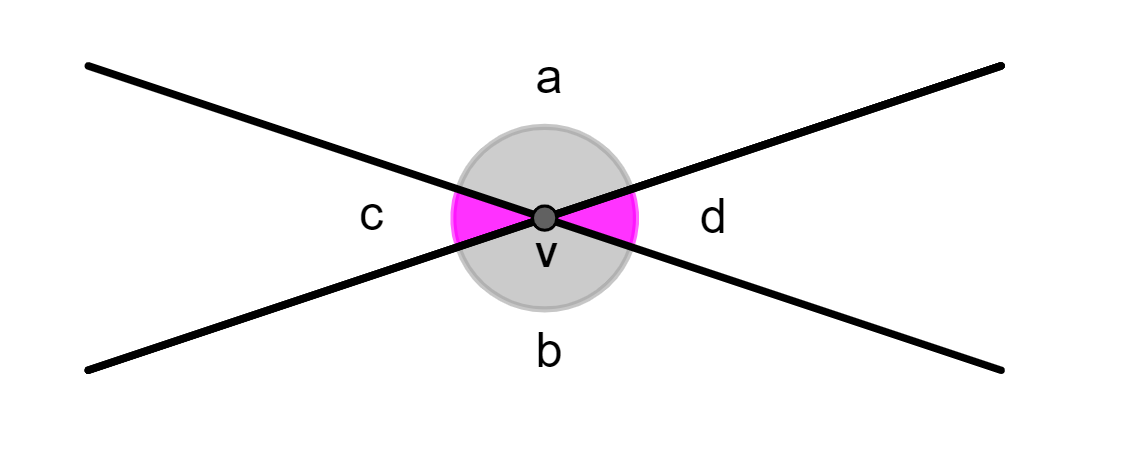
Se isso parece meio confuso, não se preocupe. A melhor forma de entender o que são ângulos o.p.v. é observando uma figura deles e associando ao nome “opostos pelo vértice”. Veja:
Na figura, temos o vértice v e os ângulos a, b, c e d, em que:
- a e b são o.p.v.
- c e d são o.p.v.
Propriedades dos ângulos opostos pelo vértice
1) Dois ângulos opostos pelo vértice são congruentes, isto é, eles têm a mesma medida em graus.
Desse modo, na figura anterior, temos:
- a = b
- c = d
2) Os ângulos adjacentes são suplementares, ou seja, juntos formam um ângulo de 180°.
Assim, temos:
- a + c = 180°
- c + b = 180°
- b + d = 180°
- d + a = 180°
Exemplos:
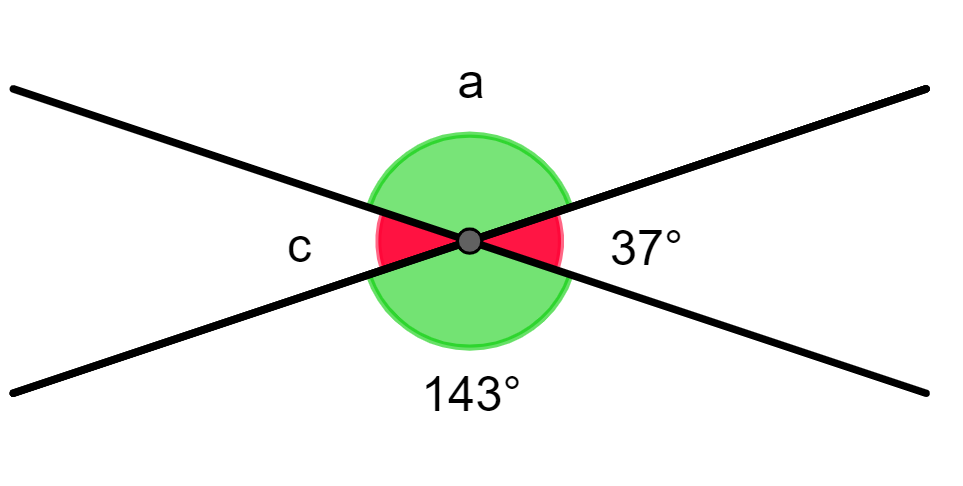
a) Determinar o valor de a e c, na figura abaixo:
Os ângulos a e 143° são o.p.v., então, pela Propriedade 1, eles têm a mesma medida. Logo:
a = 143°
Os ângulos c e 37° também são o.p.v., assim:
c = 37°
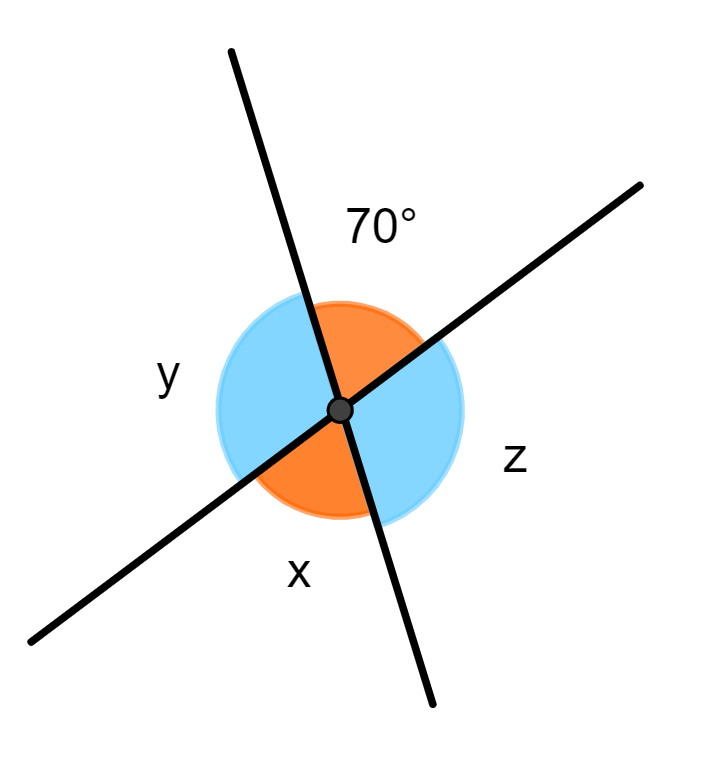
b) Determinar o valor de x, y e z na figura a seguir:
Os ângulos x e 70° são o.p.v., utilizando a Propriedade 1, da congruência entre eles, temos que:
x = 70°
Os ângulos y e 70° são adjacentes, então considerando a Propriedade 2, eles são suplementares. Portanto, temos que:
y + 70° = 180°
y = 180° – 70°
y = 110°
Os ângulos y e z são o.p.v., assim:
z = y
z = 110°
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.