Área do círculo
Saiba a definição de um círculo, veja exemplos de como calcular sua área e entenda a diferença entre ele e uma circunferência.
Desde pequenos já começamos a nos familiarizar com a ideia de um círculo. Por isso, mesmo que muitas pessoas não saibam definir essa figura geométrica, a maior parte é capaz de reconhecê-la ao seu redor:
A forma da pizza, que comumente pedimos nos finais de semana, é a de um círculo. Uma moeda, dessas que usamos diariamente para pagar um cafézinho, também tem formato de um círculo.
Mas o que é exatamente um círculo? Vamos ver!
O que é um círculo?
Um círculo é uma figura geométrica plana formada pelos pontos internos de uma circunferência.
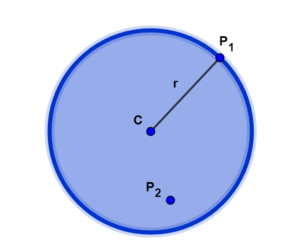
Na imagem a seguir, temos a representação de um círculo, que é limitado por uma circunferência de centro no ponto C e raio r.
Veja que a circunferência é a “borda” do círculo e qualquer ponto dela pertence ao círculo, como o ponto , e qualquer ponto interno da circunferência, como o ponto
,também faz parte do círculo.
Fórmula – Cálculo da área do círculo
A fórmula para calcular a área de um círculo com raio r é dada por:
em que é aproximadamente igual a 3,14.
Se você já conhece a fórmula para calcular a área de uma circunferência, poderá ter estranhado ao saber que a fórmula para calcular a área de um círculo é a mesma que a da circunferência.
Exemplo: Qual a área de uma praça (região circular), cujo raio mede 15 metros?
Utilizando a fórmula da área de um círculo, temos que:
Então, a área dessa praça é de 706,5 m².
Perímetro do círculo
O perímetro de um círculo nada mais é do que o perímetro da circunferência, ou seja, é o comprimento da linha. Assim, o perímetro do círculo pode ser expresso da seguinte forma:
Exemplo: Considerando a praça do exemplo anterior, quantos metros uma pessoa vai andar se der uma volta completa nela?
O perímetro da praça é exatamente a medida da sua volta completa, então, vamos calcular o perímetro:
Assim, dando uma volta completa na praça, a pessoa vai andar 94,2 m.
Diferença entre círculo e circunferência
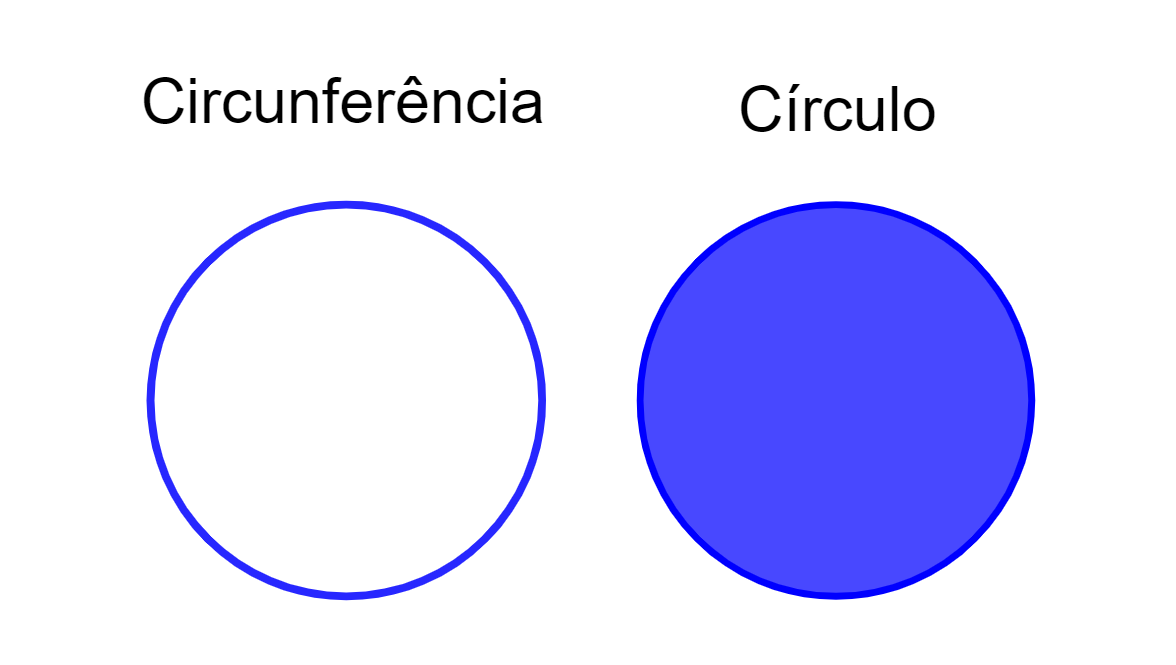
É comum a confusão entre círculo e circunferência. Para diferenciá-los, basta saber que:
A circunferência é a linha.
O círculo é a linha mais a parte interior.
Você também pode se interessar:
- Ângulos – Tipos, classificações e exemplos
- Área do trapézio – Tipos de trapézio, como calcular a área e o perímetro de um trapézio

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.