Circunferência – Definição, características e equação reduzida

Muitos objetos têm a forma de uma circunferência: as rodas de um carro, um anel, a borda de um relógio, o volante de um automóvel e vários outros. Saiba a definição, as características e a equação reduzida dessa importante figura geométrica.

Por Elainy Marciano Publicado em 23/01/2020 - 23:10

Muitos objetos têm a forma de uma circunferência: as rodas de um carro, um anel, a borda de um relógio, o volante de um automóvel e vários outros.

Você sabia que ela é a única figura plana que pode ser rodada em torno de um ponto sem aparentar que sua posição foi modificada?

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Ficou curioso e quer aprender mais sobre uma circunferência? Esse artigo é pra você!

Definição de circunferência

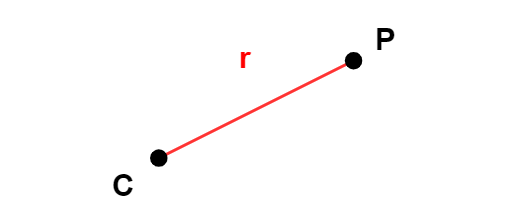
Considere um ponto C do plano e um outro ponto que está a uma distancia r de C:

Marcando todos os pontos do plano que se distanciam do ponto C exatamente a medida r, obtemos a seguinte figura geométrica:

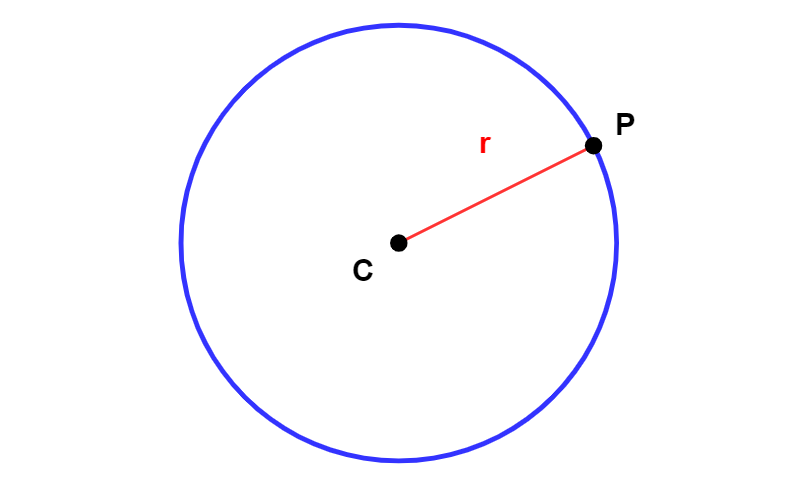
circunferencia-raio — Circunferência de raio r e centro C

Essa linha que se formou é chamada de circunferência de raio r e centro no ponto C.

Em resumo, o que é uma circunferência? Uma circunferência é definida como o conjunto de todos os pontos equidistantes (que possuem a mesma distância) de um mesmo ponto fixo no plano cartesiano.

Características de uma circunferência

Área da circunferência – A área de uma circunferência de raio r é dada por:

$\dpi{120} \bg_green A=\pi \cdot r^2$

Perímetro (comprimento) da circunferência – O perímetro de uma circunferência é a medida do contorno, ou seja, o tamanho da linha. É dado por:

$\dpi{120} \bg_green P=2\cdot \pi\cdot r$

(o valor de $\dpi{120} \pi$ é aproximadamente igual a 3,14)

Exemplo: Para uma circunferência de raio igual a 5 metros , temos que :

$\dpi{120} A= 3,14 \cdot 5^2 = 78,5 \ \textnormal{m}^2$ .
$\dpi{120} P= 2 \cdot 3,14 \cdot 5 = 31,4 \ \textnormal{m}$ .

Equação reduzida de uma circunferência

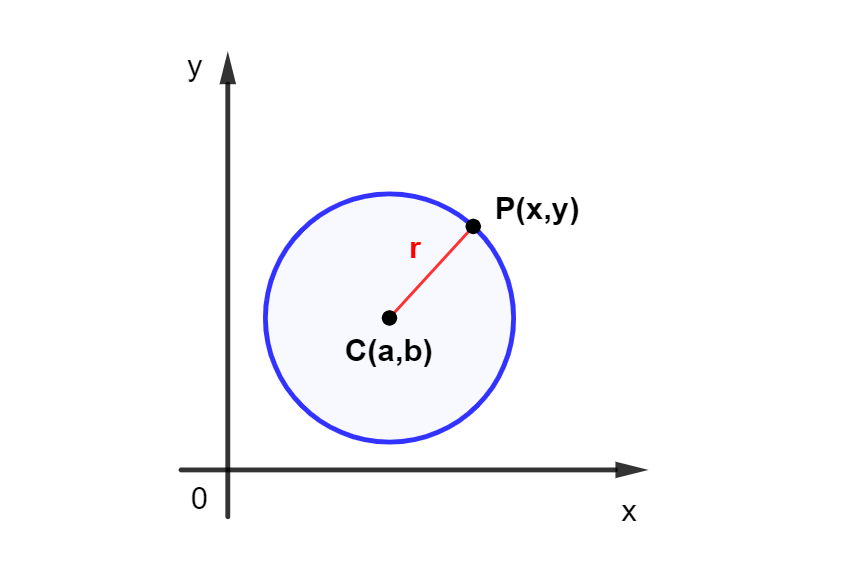
Seja P(x,y) um ponto qualquer de uma circunferência de centro C(a,b), então a distância entre os pontos C e P é igual ao raio (r) dessa circunferência.

Além disso, aplicando a fórmula geral da distância entre dois pontos quaisquer do plano, a distância entre C e P é expressa por $\dpi{120} \bg_white D_{(CP)}=\sqrt{(x-a)^2 +(y-b)^2}$ .

Unindo essas duas informações sobre a distância entre os pontos C e P, temos que:
$\dpi{120} \bg_white \sqrt{(x-a)^2 +(y-b)^2}=r.$
Elevando ao quadrado ambos os lados da equação, obtemos a equação reduzida da circunferência:
$\dpi{120} \bg_green \mathbf{(x-a)^2+(y-b)^2=r^2}$
Exemplo: Qual a equação reduzida de uma circunferência de raio 4 e centro (3,6)?

Temos que a = 3, b= 6 e r = 4 (então r² = 16).

Substituindo esses valores na fórmula, temos que a equação reduzida dessa circunferência é:

$\dpi{120} (x-3)^2+(y-6)^2=16$

Você também pode se interessar: