Lista de exercícios sobre área da coroa circular
Confira uma lista de exercícios resolvidos, passo a passo, e tire suas dúvidas sobre área da coroa circular.
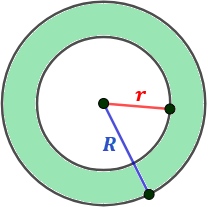
A área da coroa circular é determinada pela diferença entre a área do círculo maior e a área do círculo menor.
Veja a seguir uma lista de exercícios sobre área da coroa circular, todos resolvidos passo a passo.
Exercícios sobre área da coroa circular
Questão 1. Determine a área de uma coroa circular limitada por duas circunferências concêntricas de raios 10 cm e 7 cm.
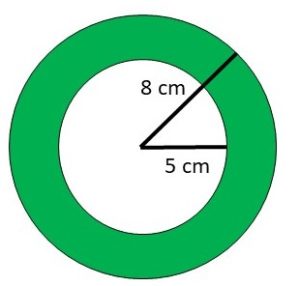
Questão 2. Calcule a área da região colorida de verde na figura abaixo:
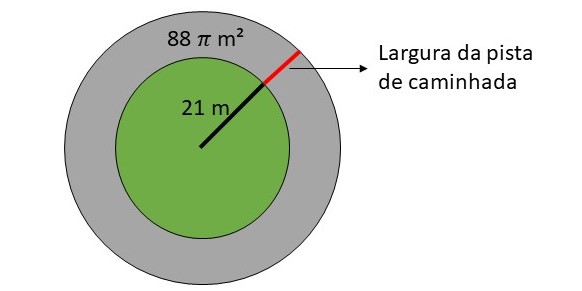
Questão 3. Em um parque com formato circular, deseja-se construir uma pista de caminhada ao seu redor. O diâmetro atual do parque é igual a 42 metros e a área da pista será de 88π m². Determine a largura da pista de caminhada.
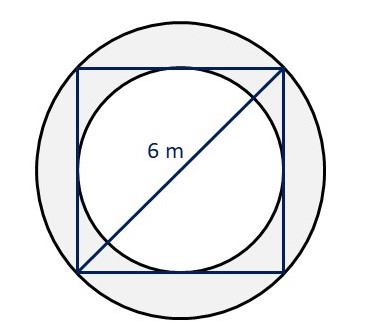
Questão 4. Determine a área de uma coroa circular formada por uma circunferência inscrita e uma circunferência circunscrita em um quadrado de diagonal igual a 6 m.
Resolução da questão 1
Temos R = 10 e r = 7. Aplicando esses valores na fórmula da área da coroa circular, temos que:
Área da coroa = π . (10² – 7²)
⇒ Área da coroa = π . (100 – 49)
⇒ Área da coroa = π . 51
Considerando π = 3,14, temos que:
Área da coroa = 160,14
Portanto, a área da coroa circular é igual a 160,14 cm².
Resolução da questão 2
Pela ilustração, temos duas circunferências de mesmo centro, com raios r = 5 e R = 8, e a área verde é a área de uma coroa circular.
Aplicando esses valores na fórmula da área da coroa circular, temos que:
Área da coroa = π . (8² – 5²)
⇒ Área da coroa = π . (64 – 25)
⇒ Área da coroa = π . 39
Considerando π = 3,14, temos que:
Área da coroa = 122,46
Portanto, a área da coroa circular é igual a 122,46 cm².
Resolução da questão 3
A partir das informações dadas, construímos um desenho representativo:
Pela ilustração, podemos ver que a largura da pista corresponde ao raio do círculo maior menos o raio do círculo menor, ou seja:
Largura = R – r
Sabemos que o diâmetro do parque (círculo) verde é igual a 42 metros, logo, r = 21 m. Assim:
Largura = R – 21
Contudo, precisamos descobrir o valor de R. Sabemos que a área da coroa é 88π m², então, vamos substituir esse valor na fórmula da área da coroa.
Área da coroa = π . (R² – r²)
⇒ 88π = π . (R² – 21²)
⇒ 88 = R² – 21²
⇒ R² = 88 + 21²
⇒ R² = 88 + 441
⇒ R² = 529
⇒ R = 23
Agora, determinamos a largura da pista de caminhada:
Largura = R – 21 = 23 – 21 = 2
Portanto, a largura da pista é igual a 2 metros.
Resolução da questão 4
A partir das informações dadas, construímos um desenho representativo:
Observe que o raio do círculo maior é metade da diagonal do quadrado, ou seja:
R = d/2
Como d = 6 ⇒ R = 6/2 ⇒R = 3.
Já o raio do círculo menor corresponde a metade da medida do lado L do quadrado:
r = L/2
Contudo, não conhecemos a medida do lado do quadrado e precisamos determiná-la primeiro.
Pelo teorema de Pitágoras, pode ser verificado que a diagonal e o lado do quadrado estão relacionados da seguinte forma:
d = L√2
Como d = 6 ⇒6 = L√2 ⇒L = 6/√2.
Portanto:
r = 6/2√2 ⇒ r = 3/√2.
Já podemos calcular a área da coroa circular:
Área da coroa = π . (R² – r²)
⇒ Área da coroa = π . (3² – (3/√2)²)
⇒ Área da coroa = π . (9 – 9/2)
⇒ Área da coroa = π . 9/2
Considerando π = 3,14, temos que:
Área da coroa = 14,13
Portanto, a área da coroa circular é igual a 14,13 m².
Para baixar essa lista sobre área da coroa circular em PDF, clique aqui!
Você também pode se interessar:
- Exercícios sobre equação da circunferência
- Exercícios sobre comprimento da circunferência
- Elementos da circunferência
- Diferença entre circunferência, círculo e esfera

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.