Teorema de Pitágoras – História, fórmula, Triângulo Pitagórico

O Teorema de Pitágoras é um dos mais famosos da Matemática e tem aplicações em diversas ciências.

É um importante teorema que permite descobrir a medida desconhecida de um dos lados de um triângulo retângulo quando conhecemos a medida dos outros dois lados.

Essa relação entre as medidas dos lados de um triângulo retângulo é extremamente útil. Por exemplo, com o Teorema de Pitágoras, a altura de uma enorme árvore, pode ser calculada mais facilmente, já que a árvore forma com o solo um ângulo reto (90º).

Quer entender melhor esse teorema e saber como ele funciona? Explicamos tudo a seguir!

História do Teorema de Pitágoras

O Teorema de Pitágoras recebeu esse nome em homenagem a Pitágoras, um grande matemático e filósofo grego que viveu entre 570 a. C. e 495 a. C.

Apesar de ter sido nomeado dessa forma e Pitágoras receber os créditos de descobridor do teorema, existem argumentos de que o Teorema de Pitágoras já fosse conhecido muito antes da existência do matemático.

Um fato curioso sobre o Teorema de Pitágoras é que foi a partir da aplicação dele, em um triângulo de catetos com medida igual a 1, que foi descoberto o primeiro número irracional ().

Fórmula do Teorema de Pitágoras

Para entender a fórmula do teorema de Pitágoras é muito importante saber o que é um triângulo retângulo.

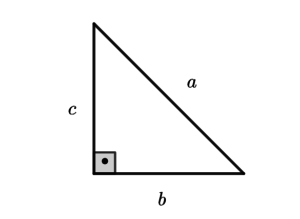
Triângulo Retângulo: triângulo que possui um ângulo interno reto (ângulo de 90º). Os outros dois ângulos são agudos, medem menos que 90º.

O maior lado do triângulo, oposto ao ângulo de 90º, é chamado de hipotenusa (a) e os outros dois lados são chamados de catetos (b e c).

O Teorema de Pitágoras nos diz que a hipotenusa ao quadrado é igual a soma dos quadrados dos catetos. Então, a fórmula do teorema de Pitágoras é:

Em que:

•  → hipotenusa;
•  → catetos.

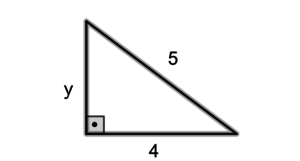
Exemplo: Vamos aplicar o Teorema de Pitágoras para encontrar o valor desconhecido no triângulo abaixo:

Temos que:  ,  e  é um valor desconhecido que queremos encontrar.

Aplicando o Teorema de Pitágoras, temos que:

Então, .

Triângulo Pitagórico

Quando as medidas a, b e c, dos lados de um triângulo são números inteiros que satisfazem o Teorema de Pitágoras, isto é,

dizemos que os números a, b e c formam um terno pitagórico e que esse triângulo é um Triângulo Pitagórico.

Exemplo: Se a = 13, b = 12 e c = 5 são as medidas dos lados de um triângulo retângulo, temos um Triângulo Pitagórico, pois a, b e c são números inteiros e

• 
• 

Satisfaz o Teorema de Pitágoras: .

Você também pode se interessar:

• Exercícios sobre Teorema de Pitágoras
• Ângulos – Tipos, classificações e exemplos
• Circunferência – Definição, características e equação reduzida