Exercícios sobre Teorema de Pitágoras

Vários exercícios resolvidos utilizando o Teorema de Pitágoras.

Por Elainy Marciano Publicado em 04/02/2020 - 16:24

Os exercícios, a seguir, são referentes ao Teorema de Pitágoras, um importante teorema que relaciona as medidas dos lados de um triângulo retângulo.

Questão 1. Em um triângulo retângulo as medidas dos catetos são 24 e 32. Quanto mede a hipotenusa desse triângulo?

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Questão 2. Os lados de um triângulo medem 12 cm, 35 cm e 37 cm. Podemos dizer que esse triângulo é um triângulo retângulo?

Questão 3. Os lados de um triângulo medem 10 cm, 16 cm e 22 cm. Podemos dizer que esse triângulo é um triângulo retângulo?

Questão 4. Se as medidas dos catetos de um triângulo são ( $\bg_white 2-\sqrt{5}$ ) e ( $\bg_white 2 +\sqrt{5}$ ), quanto mede a hipotenusa?

Questão 5. O valor da hipotenusa de um triângulo retângulo é 20, o cateto menor é 3x e o cateto maior, 4x. Encontre o valor de x.

Questão 6. O valor da hipotenusa de um triângulo retângulo é (x + 1), o cateto menor é $\bg_white \sqrt{7}$ e o cateto maior, x . Encontre o valor de x.

Questão 7. Um terreno em forma retangular tem 20 metros de comprimento e 12 metros de largura. Quanto mede a diagonal desse terreno?

Questão 8. Um terreno triangular tem frentes de 8 m e 15 m em duas ruas que formam um ângulo de 90°. Quanto mede o terceiro lado desse terreno?

Questão 9. Utilizando o Teorema de Pitágoras, determine a altura de um triângulo equilátero de lado 15 cm.

Questão 10. Para alcançar o galho mais alto de uma árvore, foi utilizada uma escada de 7 metros com sua base colocada a 3,4 metros de distância da árvore. A que altura, do chão, esse galho se encontra?

Solução da Questão 1

Trata-se de um triângulo retângulo, então podemos utilizar o Teorema de Pitágoras. Sendo $\dpi{120} \bg_white a$ a hipotenusa desse triângulo, temos que:

$\dpi{120} \flushleft a^2=24^2+32^2\\ a^2=1600 \\ a = \sqrt{1600} \\ a = 40$

O valor da hipotenusa desse triângulo é 40.

Solução da Questão 2

O que temos que verificar é se as medidas dos lados desse triângulo satisfazem o Teorema de Pitágoras, ou seja,

$\dpi{120} \bg_white a^2=b^2+c^2$

Então, vamos verificar:

A hipotenusa é o lado oposto ao maior ângulo de um triângulo retângulo (o ângulo de 90º). Assim, o maior lado de um triângulo retângulo é sempre a hipotenusa. Logo, $\dpi{120} \bg_white a=37$ . Já os valores dos catetos são: $\dpi{120} \bg_white b=12$ e $\dpi{120} \bg_white c=35$ . Substituindo na fórmula, temos que:

$\bg_white a^2 = 37^2 = 1369$ e
$\bg_white b^2 +c^2 = 12^2 +35^2 = 144 +1225 = 1369$

Então, satisfaz o Teorema de Pitágoras. Logo, podemos dizer que é um triângulo retângulo.

Solução da Questão 3

Semelhante ao que foi feito na questão 2, vamos verificar se satisfaz o Teorema de Pitágoras.

Temos : $\dpi{120} \bg_white a=22$ , $\dpi{120} \bg_white b=10$ e $\dpi{120} \bg_white c=16$ . Então:

$\bg_white a^2 = 22^2 = 484$ e
$\bg_white b^2 +c^2 = 10^2 +16^2 = 100 + 256 = 356$

Assim, $\bg_white a^2 \neq b^2 + c^2$ . Portanto, não satisfaz o Teorema de Pitágoras e não é, então, um triângulo retângulo.

Solução da Questão 4

Aplicando o Teorema de Pitágoras, temos que:

$\flushleft a^2 = b^2 + c^2\\ a^2 = (2+ \sqrt{5})^2 + (2- \sqrt{5})^2\\ a^2 = (2^2 +2\sqrt{5} + (\sqrt{5})^2) + (2^2 -2\sqrt{5} + (\sqrt{5})^2) \\ a^2 = 4 +2\sqrt{5} + 5 + 4 -2\sqrt{5} + 5 \\ a^2 = 18\\ a = \sqrt{18}\\ a \approx 4,24$

A hipotenusa é aproximadamente igual a 4,24.

Solução da Questão 5

Temos o seguinte triângulo retângulo:

Aplicando o Teorema de Pitágoras, temos que:

$\flushleft a^2 = b^2 +c^2 \\ 20^2 = (3\mathrm{x})^2 + (4\mathrm{x})^2 \\ 400 = 9x^2 + 16 \mathrm{x}^2 \\ 400 = 25x^2 \\ x^2 = 400/25 \\ x^2 = 16 \\ x = \sqrt{16}\\ x = 4$

Então, x = 4 e os catetos têm valores 12 e 16.

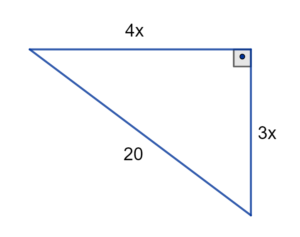
Solução da Questão 6

Essa questão é semelhante a anterior. Vamos utilizar o Teorema de Pitágoras:

$\bg_white \flushleft (x + 1)^2 = (\sqrt{7})^2 +\mathrm{x}^2 \\ x^2 + 2\mathrm{x} + 1 = 7 + \mathrm{x}^2 \\ x^2 +2\mathrm{x} -\mathrm{x}^2 = 7 - 1\\ 2x = 6\\ x = 6/2\\ x = 3$

Então, x = 3 e o valor da hipotenusa é 4 e do cateto menor é 3.

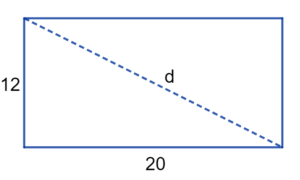
Solução da Questão 7

Traçando a diagonal de um retângulo, obtemos dois triângulos retângulos. Assim, para saber o comprimento da diagonal, tudo o que temos que fazer é descobrir o valor da hipotenusa de um triângulo retângulo com catetos com valores 20 e 12 .

Aplicando o teorema de Pitágoras:

$\dpi{120} \flushleft a^2 = b^2 +c^2\\ a^2 = 12^2+20^2\\ a^2 = 544\\ a = \sqrt{544}\\ a = 4\sqrt{34}\\ a \approx 23,32$

Então, a diagonal do terreno tem aproximadamente 23,32 metros de comprimento.

Solução da Questão 8

Se nesse triângulo, dois lados formam um ângulo de 90º, então é triângulo retângulo. Se é um triângulo retângulo, podemos aplicar o teorema de Pitágoras para encontrar o valor do outro lado.

Os valores dados são as medidas dos catetos (pois são eles que formam o ângulo de 90º, lembre que a hipotenusa é sempre oposta a esse ângulo). Assim, a medida que temos que encontrar, é a medida da hipotenusa.

$\flushleft a^2= 8^2 + 15^2 \\ a^2 = 64 + 225 \\ a^2 = 289 \\ a = \sqrt{289} \\ a = 17$

Portanto, o terceiro lado do terreno mede 17 metros.

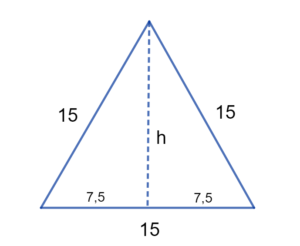
Solução da Questão 9

A altura divide esse triângulo equilátero em dois triângulos retângulos, em que a hipotenusa de cada um mede 15 cm, o cateto menor mede metade da medida do lado do triângulo equilátero, isto é, 15 cm $\bg_white \div$ 2 = 7,5 cm, e o cateto maior, que corresponde à altura, é um valor desconhecido que queremos encontrar.

Então, vamos usar o Teorema de Pitágoras:

$\bg_white \flushleft a^2 = b^2 + c^2\\ 15^2 = 7,5^2 + c^2 \\ 225 = 56,25 + c^2 \\ c^2=225-56,25\\ c^2 = 168,75 \\ c = \sqrt{168,75}\\ c \approx 12,99$

Então, o triângulo equilátero tem aproximadamente 12,99 cm de altura.

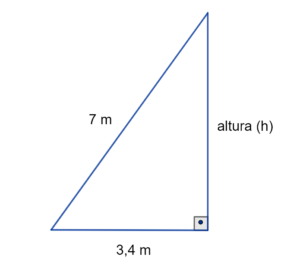
Solução da Questão 10

Conforme é apresentado na figura abaixo, temos um triângulo retângulo, pois a árvore forma, junto com o solo, um ângulo de 90º. A hipotenusa, que é o lado oposto ao ângulo de 90º graus, mede 7 m e o cateto menor mede 3,4 m.

Utilizando o Teorema de Pitágoras, vamos encontrar a medida do outro cateto, correspondente à altura do galho, em relação ao chão:

$\flushleft a^2 = b^2 +c^2 \\ 7^2 = 3,4^2 +c^2 \\ 49 = 11,56 + c^2 \\ c^2 = 49 -11,56 \\ c^2 = 37,44 \\ c = \sqrt{37,44} \\ c \approx 6,11$

Logo, o galho está a aproximadamente 6,11 metros de altura do chão.

Veja também: