Múltiplos e submúltiplos do metro – Quais são, como fazer transformação entre medidas

Você já viu alguém utilizar o palmo ou o passo para medir o comprimento de alguma coisa? Por muito tempo era dessa forma (com partes do corpo) que as pessoas expressavam medida de comprimento.

Mas, devido a necessidade de facilitar a comunicação entre comunidades científicas e comerciais no mundo todo, por volta do ano 1790, foi estabelecido o Sistema Métrico Decimal, no qual o metro, que nós utilizamos hoje em dia, é a unidade fundamental de medida.

Vamos conhecer mais sobre o metro e seus múltiplos e submúltiplos?

O Metro

O metro (m) é a unidade fundamental de medida de comprimento do Sistema Métrico Decimal.

Utilizamos o metro quando, por exemplo, queremos dizer a altura de uma pessoa, a largura de uma sala, a altura de uma casa etc.

Já para expressar grandes medidas, como a distância de uma cidade a outra, ou pequenas medidas, como a altura de uma tampinha de garrafa, temos os múltiplos e submúltiplos do metro.

Os múltiplos do metro

Para grandes distâncias, o mais adequado é utilizar os múltiplos do metro: o decâmetro, o hectômetro e o quilômetro, em que:

• 1 decâmetro (dam) = 10 metros
• 1 hectômetro (hm) = 100 metros
• 1 quilômetro (km) = 1000 metros

Os submúltiplos do metro

Para pequenas distâncias, temos os submúltiplos do metro: o decímetro, o centímetro e o milímetro, tais que:

• 1 decímetro (dm) = 0,1 metro
• 1 centímetro (cm) = 0,01 metro
• 1 milímetro (mm) = 0,001 metro

Em outras palavras:

Se dividirmos o metro em 10 partes iguais, uma dessas partes corresponde a 1 decímetro;

Se dividirmos o metro em 100 partes iguais, uma dessas partes corresponde a 1 centímetro;

Se dividirmos o metro em 1000 partes iguais, uma dessas partes corresponde a 1 milímetro.

Transformando medidas

Considere a seguinte situação:

Para chegar até o portão de casa, Ana andou 5,63 m e Laura, 423 cm. Quem percorreu a maior distância?

Para responder essa pergunta, precisamos saber a distância que cada uma percorreu, considerando a mesma unidade de medida.

Vamos transformar a distância percorrida por Ana para centímetros (também poderíamos transformar a distância percorrida por Laura para metros).

Em transformações de medida de comprimento, podemos contar com ajuda da seguinte tabelinha:

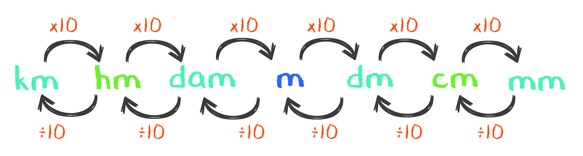
Observe que para sair de m e ir para cm, na tabelinha, temos que fazer dois “pulos” para a direita. Em cada um desses “pulos”, devemos multiplicar por 10, ou seja:

• 5,63 m  cm:

1º “pulo”: 5,63 m = (5,63 x 10) dm = 56,3 dm (No primeiro “pulo” saímos de m e chegamos em dm)

2º “pulo”: 56,3 dm = (56,3 x 10) cm = 563 cm (No segundo “pulo” saímos de dm e chegamos em cm, como queríamos)

Então, 5,63 m é igual a 563 cm. Assim, chegamos na resposta desse problema, Ana foi a que percorreu a maior distância, 563 cm.

Mas, temos uma forma mais prática de chegar nesse mesmo resultado. Veja:

Demos dois “pulos”, em cada “pulo” multiplicamos por 10. Fazer isso, é o mesmo que multiplicar diretamente por 100, já que 10 x 10 = 100. Observe:

• 5,63 m  cm:

5,63 x 100 = 563 

Então, 5,63 m = 563 cm

Vamos ver mais alguns exemplos, mas dessa vez fazendo diretamente pelo método mais prático.

Exemplos – Transformando medidas

Fazer as seguintes transformações de medidas de comprimento:

• Transformar 8 metros em milímetros: 8 m  mm

Multiplicamos por 1000, pois são três “pulos” para a direita:

8 x 1000 = 8000

Logo, 8 m = 8000 mm.

• Transformar 5 metros em decâmetros: 5 m  dam

Aqui, dividimos por 10 porque é um “pulo” para a esquerda:

5  10 = 0,5

Assim, 5 m = 0,5 dam.

• Transformar 12 centímetros em metros: 12 cm  m

Dividimos por 100, pois são dois “pulos” para a esquerda:

12  100 = 0,12

Então, 12 cm = 0,12 m.

• Transformar 1250 metros em quilômetros: 1250 m  km

Dividimos por 1000, pois são três “pulos” para a esquerda:

1250  1000 = 1,250

Desse modo, 1250 m = 1,250 km.

Para memorizar:

Se vou para a direita, então multiplico. Se vou para a esquerda, então divido.

Multiplico e divido por quanto? 10 para 1 “pulo”, 100 para 2 “pulos” e 1000 para 3 “pulos”.

 

Leia também:

• Multiplicação de números decimais – Aprenda a multiplicar números com vírgula
• Como transformar quilômetros em milhas? – Fórmula e exemplos
• Como escrever um número na notação científica? – Mudando a posição da vírgula e exemplos