Números Inteiros

Os números inteiros são formados por todos os números que não são decimais. Ou seja, são todos os números positivos e negativos.

Como o número 5, por exemplo, pertence ao conjunto dos números naturais e dos números inteiros. Já o número –5 pertence apenas ao conjunto dos números inteiros, pois é o número oposto do natural 5. Por isto, quando adicionamos ou subtraímos números inteiros o resultado ainda será um inteiro.

A letra Z é usada para representar os números Inteiros. Confira o exemplo abaixo:

ℤ = {…, – 6, – 5, – 4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, …}

Ao lado, podemos notar que todos os números inteiros estão dentro do diagrama, assim como os negativos podem ser agrupados. Esta junção se denomina como Conjunto dos Números Naturais.
Assim podemos determinar também, que os Números Inteiros são:

• Z – É formado por todos os números inteiros negativos. Logo, o número zero não pertence a esse conjunto.
• Z + É formado por todos os números inteiros não negativos (positivos), ou seja, pelo próprio conjunto dos números naturais. Logo, Z + = N.
• Z* é formado por todos os números inteiros, com exceção do zero.

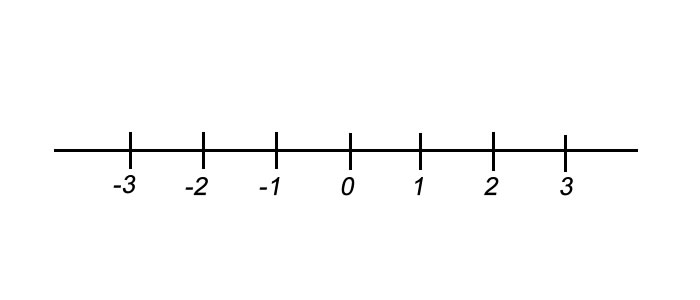
Reta numérica dos Inteiros:

Colocando sobre uma Reta, os números Inteiros são dispostos num ponto, cujo número mediano é zero. A regra para a construção dessa reta numérica é que, os números devem ser colocados em uma sequência crescente, da direita para a esquerda.

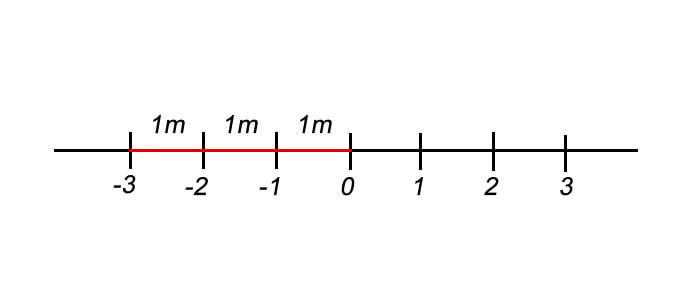
Por exemplo: suponha que a unidade de medida escolhida seja o metro, começando pelo ponto mediano 0, os próximos serão 1,2,3,4 e assim por diante… A distância entre o número 1 e o número 2 é igual a 1 metro, dado a distância entre os dois números consecutivos sempre serem iguais na unidade de medida utilizada. Porém a distância entre – 2m e 2m é de 4 metros. Por estes motivos, podemos concluir que – 2 < 1.

Valor absoluto e Módulo absoluto:

O módulo é a distância entre zero e o número observado na unidade de medida em que a reta foi construída. Como não existem distâncias negativas, o módulo sempre será um número positivo para qualquer número entre módulos. Além disso, o módulo de um número é representado por esse número entre duas barras, como em: | – 3| = 3

Confira também:

• Números Naturais
• Números Racionais