Ponto médio de um segmento de reta

Entenda o que é o ponto médio de um segmento de reta e como calcular as coordenadas desse ponto. Veja as fórmulas e exemplos.

Por Elainy Marciano Publicado em 12/11/2020 - 16:11

Em geometria, um segmento de reta é definido como uma parte da reta, que possui começo e fim. O ponto de origem e o ponto final do segmento são chamados de extremidades do segmento de reta.

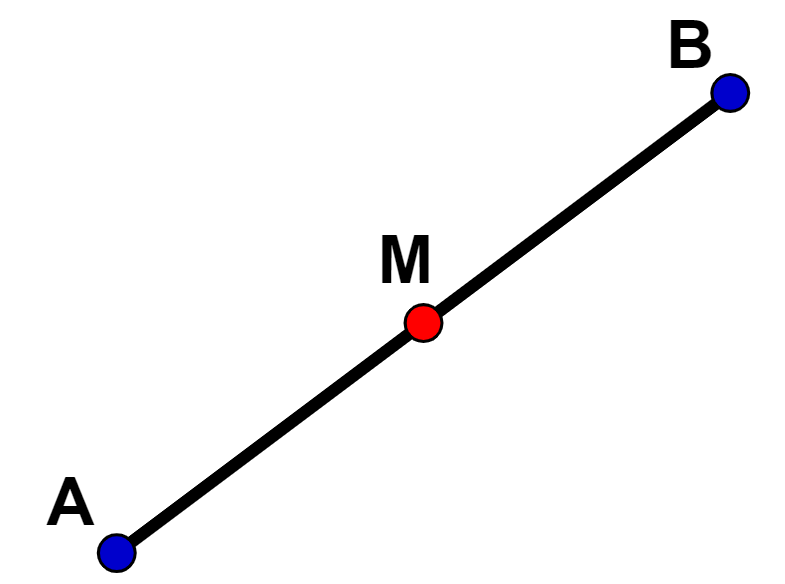
Dado um segmento de reta qualquer com extremidades A e B, o ponto M que divide o segmento em duas partes iguais é chamado de ponto médio.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Coordenadas do ponto médio

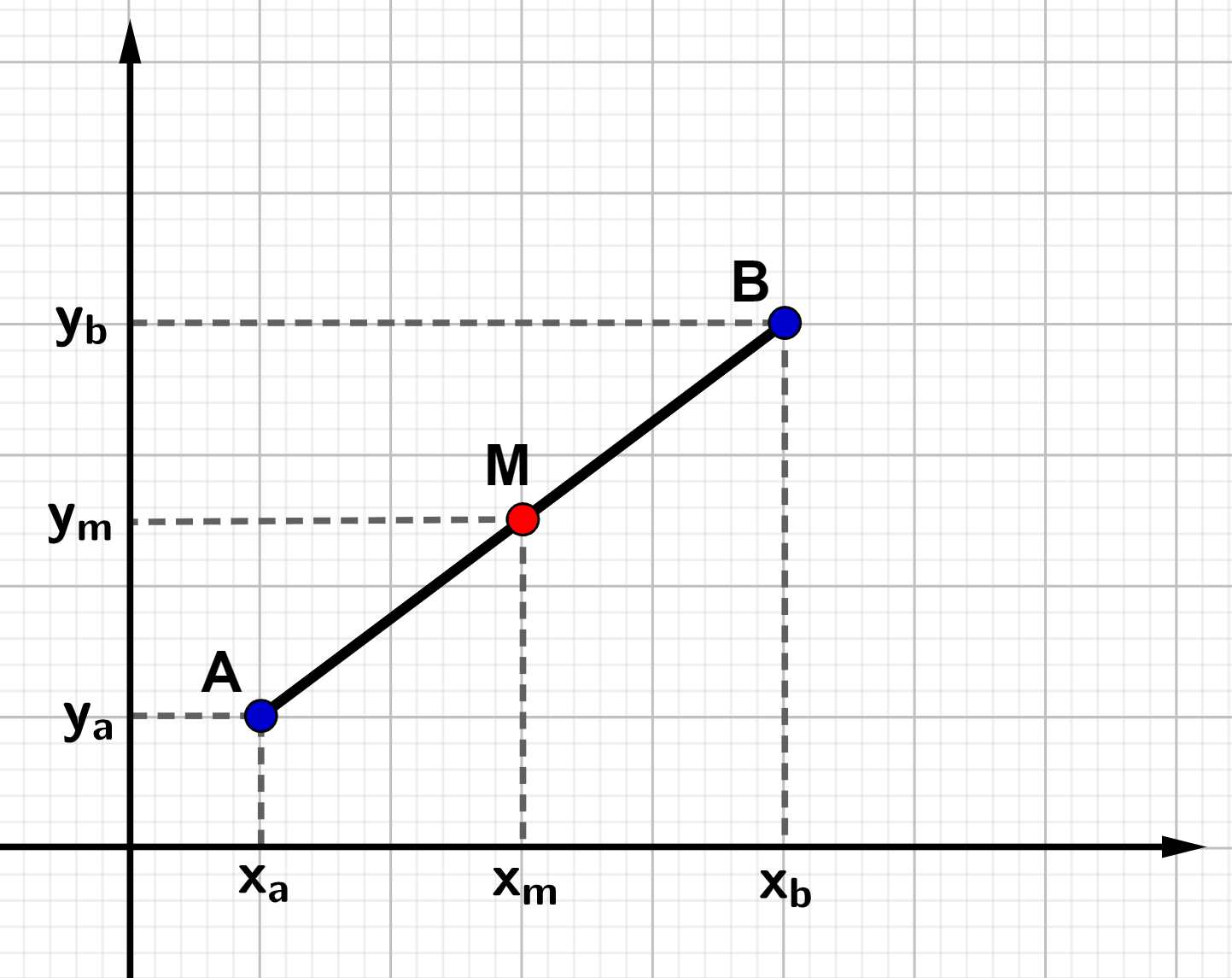
Considerando o segmento de reta no plano cartesiano, podemos determinar as coordenadas do ponto médio.

Em um segmento com extremidades $\dpi{120} \mathbf{A(x_a,y_a)}$ e $\dpi{120} \mathbf{B(x_b,y_b)}$ , as coordenadas do ponto médio $\dpi{120} \mathbf{M(x_m,y_m)}$ podem ser obtidas a partir de duas fórmulas.

A abscissa do ponto médio é dada por:

$\dpi{120} \mathbf{x_m = \frac{x_a+x_b}{2}}$

E a ordenada do ponto é dada por:

$\dpi{120} \mathbf{y_m = \frac{y_a+y_b}{2}}$

Exemplo 1:

Determine as coordenadas do ponto médio do segmento com extremidades A(1, 3) e B(3, 5).

$\dpi{120} \mathrm{x_m = \frac{1+3}{2} = \frac{4}{2}=2}$

$\dpi{120} \mathrm{y_m = \frac{3+5}{2} = \frac{8}{2}=4}$

Portanto, o ponto médio é M(2, 4).

Exemplo 2:

Determine as coordenadas do ponto médio do segmento com extremidades C(-2, 3) e D(4, -2).

$\dpi{120} \mathrm{x_m = \frac{-2+4}{2} = \frac{2}{2}=1}$

$\dpi{120} \mathrm{y_m = \frac{3-2}{2} = \frac{1}{2}}$

Portanto, o ponto médio é M(1, 1/2).

Exemplo 3:

O ponto M(5, 1/2) é o ponto médio do segmento de origem A(3, -1). Determine as coordenadas da outra extremidade do segmento.

Sendo B(x, y) a outra extremidade do segmento, pela fórmula das coordenadas do ponto médio, temos que:

$\dpi{120} \mathrm{5 = \frac{3 + x}{2}}$

$\dpi{120} \mathrm{\Rightarrow 5\cdot 2 = 3 + x}$

$\dpi{120} \mathrm{\Rightarrow 10= 3 + x}$

$\dpi{120} \mathrm{\Rightarrow x = 10-3}$

$\dpi{120} \mathrm{\Rightarrow x = 7}$

Além disso, temos que:

$\dpi{120} \mathrm{\frac{1}{2} = \frac{-1 + y}{2}}$

$\dpi{120} \mathrm{\Rightarrow 1 = -1 + y}$

$\dpi{120} \mathrm{\Rightarrow y = 1+ 1}$

$\dpi{120} \mathrm{\Rightarrow y =2}$

Portanto, a outra extremidade do segmento é o ponto B(7,2).

Você também pode se interessar:

Geometria analítica

Elainy Marciano

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.