Produtos notáveis

O produtos notáveis aparecem o tempo todo em expressões algébricas e conhecê-los vai te ajudar em muitas contas. Por isso, confira esse post e aprenda sobre produtos notáveis.

Por Elainy Marciano Publicado em 19/03/2020 - 16:54

O que são produtos notáveis? Os produtos notáveis são multiplicações que aparecem com frequência em cálculos algébricos.

Confira abaixo quais são suas propriedades e aprenda como aplicar a propriedade distributiva.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Principais produtos notáveis

Os principais produtos notáveis são:

→ Quadrado da soma de dois termos: $\dpi{120} (x+y)^2=(x+y)\cdot (x+y)$ → Quadrado da diferença de dois termos:

$\dpi{120} (x-y)^2=(x-y)\cdot (x-y)$

→ Produto da soma pela diferença de dois termos:

$\dpi{120} (x+y)\cdot (x-y)$

→ Cubo da soma de dois termos:

$\dpi{120} (x+y)^3=(x+y)\cdot (x+y)\cdot(x+y)$

→ Cubo da diferença de dois termos:

$\dpi{120} (x-y)^3=(x-y)\cdot (x-y)\cdot(x-y)$

Propriedades dos produtos notáveis

Podemos desenvolver de forma algébrica cada um dos produtos notáveis, obtendo expressões que vão facilitar muitos cálculos envolvendo esses produtos.

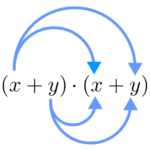
Quadrado da soma de dois termos

$\dpi{120} \boldsymbol{(x+y)^2=(x+y)\cdot (x+y)}$

Aplicando a propriedade distributiva:

$\dpi{120} = x^2+xy+xy+y^2$

$\dpi{120} = x^2+2xy+y^2$

Então, temos que:

$\dpi{120} \bg_green \boldsymbol{\boldsymbol{}(x+y)^2= x^2+2xy+y^2}$

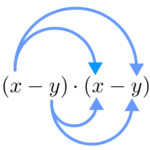
Quadrado da diferença de dois termos

$\dpi{120} \boldsymbol{(x-y)^2=(x-y)\cdot (x-y)}$

Aplicando a propriedade distributiva:

$\dpi{120} = x^2-xy-xy+y^2$

$\dpi{120} = x^2-2xy+y^2$

Então, temos que:

$\dpi{120} \bg_green \boldsymbol{\boldsymbol{}(x-y)^2= x^2-2xy+y^2}$

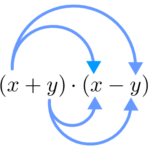
Produto da soma pela diferença de dois termos

$\dpi{120} \boldsymbol{(x+y)\cdot (x-y)}$

Aplicando a propriedade distributiva:

$\dpi{120} =x^2-xy+xy-y^2$

$\dpi{120} =x^2-y^2$

Então, temos que:

$\dpi{120} \bg_green \boldsymbol{\boldsymbol{}(x+y)\cdot (x-y)= x^2-y^2}$

Cubo da soma de dois termos

$\dpi{120} \boldsymbol{(x+y)^3=(x+y)\cdot (x+y)\cdot(x+y)}$

Utilizando a propriedade do quadrado da soma de dois termos:

$\dpi{120} (x+y)^3=(x+y)\cdot (x^2+2xy+y^2)$

$\dpi{120} =x^3+2x^2y+xy^2+x^2y+2xy^2+y^3$

$\dpi{120} =x^3+3x^2y+3xy^2+y^3$

Então, temos que:

$\dpi{120} \bg_green \boldsymbol{\boldsymbol{}(x+y)^3= x^3+3x^2y+3xy^2+y^3}$

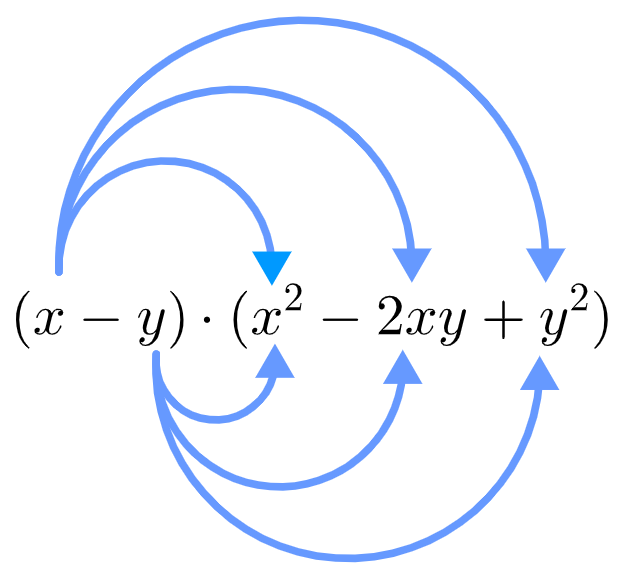
Cubo da diferença de dois termos

$\dpi{120} \boldsymbol{(x-y)^3=(x-y)\cdot (x-y)\cdot(x-y)}$

Utilizando a propriedade do quadrado da diferença de dois termos:

$\dpi{120} (x-y)^3=(x-y)\cdot (x^2-2xy+y^2)$

$\dpi{120} =x^3-2x^2y+xy^2-x^2y+2xy^2-y^3$

$\dpi{120} =x^3-3x^2y+3xy^2-y^3$

Então, temos que:

$\dpi{120} \bg_green \boldsymbol{\boldsymbol{}(x-y)^3= x^3-3x^2y+3xy^2-y^3}$

Quadro resumo dos produtos notáveis

Resumindo todas essas propriedades dos produtos notáveis, temos um quadro resumo:

Quadro resumo produtos notáveis — Quadro resumo dos produtos notáveis.

Clique aqui para baixar esse quadro resumo em PDF!

Você também pode se interessar:

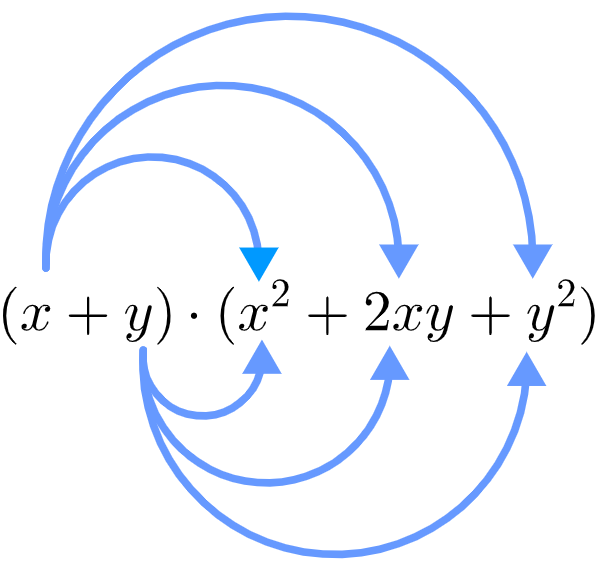
Cubo da diferença de dois termos Cubo da soma de dois termos Produto da soma pela diferença de dois termos Produtos notáveis Quadrado da diferença de dois termos Quadrado da soma de dois termos

Elainy Marciano

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.