Relações métricas no triângulo retângulo

Além do Teorema de Pitágoras, temos outras cinco relações muito importantes entre as medidas de um triângulo retângulo. Aprenda quais são e como usar.

Por Elainy Marciano Publicado em 31/01/2020 - 16:28

As relações métricas em um triângulo são as relações existentes entre as suas medidas.

No triângulo retângulo, a relação mais famosa é dita pelo Teorema de Pitágoras. Mas, além dessa, existem outras cinco relações muito úteis, que possibilitam resolver uma porção de problemas envolvendo esse tipo de triângulo.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Antes de apresentar as relações métricas do triângulo retângulo, é importante entender alguns conceitos: os elementos de um triângulo retângulo e semelhança entre triângulos no triângulo retângulo.

Elementos de um triângulo retângulo

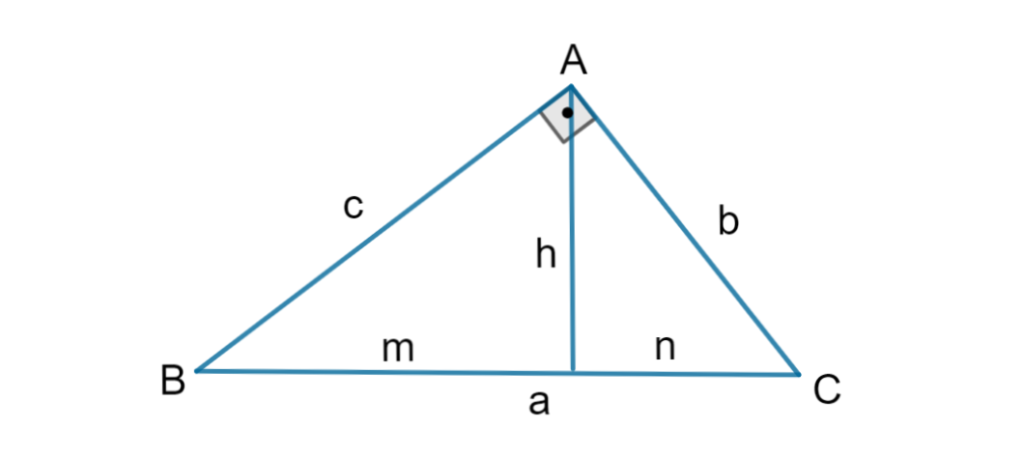
Os elementos de um triângulo retângulo são:

a → hipotenusa
b → cateto
c → cateto
h → altura do triângulo (relativa à hipotenusa)
m → projeção do cateto c sobre a hipotenusa
n → projeção do cateto b sobre a hipotenusa

Triângulos semelhantes em um triângulo retângulo

Observe que a altura (h) divide o triângulo ABC, apresentado anteriormente, em outros dois triângulos:

Temos uma propriedade muito interessante entre os triângulos ABC, HBA e HAC: eles são triângulos semelhantes.

Triângulos semelhantes possuem ângulos correspondentes com a mesma medida e lados correspondentes proporcionais.

Relações métricas no triângulo retângulo

Relação 1. Da semelhança entre os triângulos ABC e HBA, temos que:

$\dpi{120} \bg_white \frac{a}{c}=\frac{c}{m}\Rightarrow c^2=a\cdot m$

Essa relação nos diz que o quadrado do cateto c é igual ao produto entre a hipotenusa e a projeção desse cateto.

Relação 2. Da semelhança entre os triângulos ABC e HAC, temos que:

$\dpi{120} \bg_white \frac{a}{b}=\frac{b}{n}\Rightarrow b^2=a\cdot n$

É similar a relação anterior, ela nos diz que o quadrado do cateto b é igual ao produto entre a hipotenusa e a projeção desse cateto.

Relação 3. Da semelhança entre os triângulos ABC e HBA (ou dos triângulos ABC e HAC), temos que:

$\dpi{120} \bg_white \frac{a}{b}=\frac{c}{h}\Rightarrow a\cdot h=c\cdot b$

Por essa relação, temos que o produto entre a hipotenusa e a altura é igual ao produto entre os catetos.

Relação 4. Da semelhança entre os triângulos HBA e HAC, temos que:

$\dpi{120} \bg_white \frac{m}{h}=\frac{h}{n}\Rightarrow h^2=m\cdot n$

Aqui, temos que o quadrado da altura é igual ao produto das projeções dos catetos.

Relação 5. Essa é, sem dúvidas, a relação mais simples de ser verificada. Observe no triângulo retângulo ABC que:

$\dpi{120} \bg_white a = m +n$

Ou seja, nos diz que a hipotenusa é igual a soma das projeções dos catetos.

Teorema de Pitágoras

Relação 6. Pelo Teorema de Pitágoras, temos que: o quadrado da hipotenusa é igual a soma dos quadrados dos catetos, isto é,

$\dpi{120} \bg_white a^2 = b^2 +c^2$

Quando devemos usar o Teorema de Pitágoras? Quando queremos encontrar a medida de um dos lados do triângulo, sendo conhecidas as medidas dos seus outros dois lados.