Lista de exercícios sobre semelhança de triângulos
Preparamos uma lista de exercícios resolvidos sobre triângulos semelhantes. Confira para aprender mais sobre esse assunto!
Triângulos semelhantes são triângulos que possuem os três ângulos correspondentes com a mesma medida e os lados proporcionais.
A divisão das medidas dos lados proporcionais é um valor constante, chamado de razão de proporcionalidade.
Existem alguns casos específicos para identificar triângulos semelhantes:
Caso 1) Ângulo – Ângulo (AA)
Caso 2 ) Lado – Lado – Lado (LLL)
Caso 3) Lado – Ângulo – Lado (LAL)
Além disso, devemos nos lembrar do teorema fundamental da semelhança entre triângulos:
Se traçarmos uma reta que intersecta dois lados de um triângulo em pontos diferentes e que seja paralela ao terceiro lado do triângulo, obtemos um outro triângulo que é semelhante ao primeiro.
Para aprender mais sobre esse assunto, confira uma lista de exercícios sobre semelhança de triângulos.
Lista de exercícios sobre semelhança de triângulos
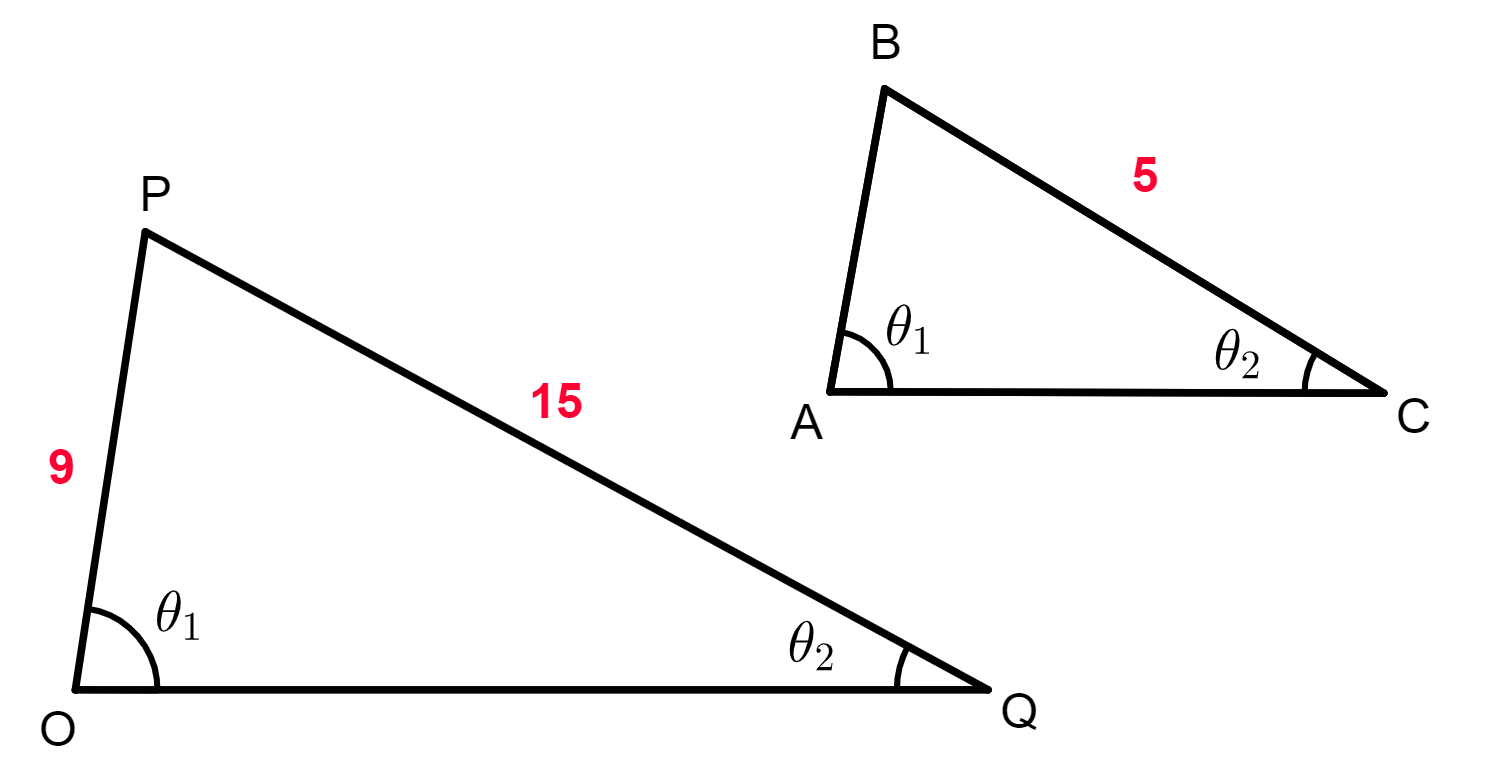
Questão 1. Determine o valor do segmento AB na figura abaixo:
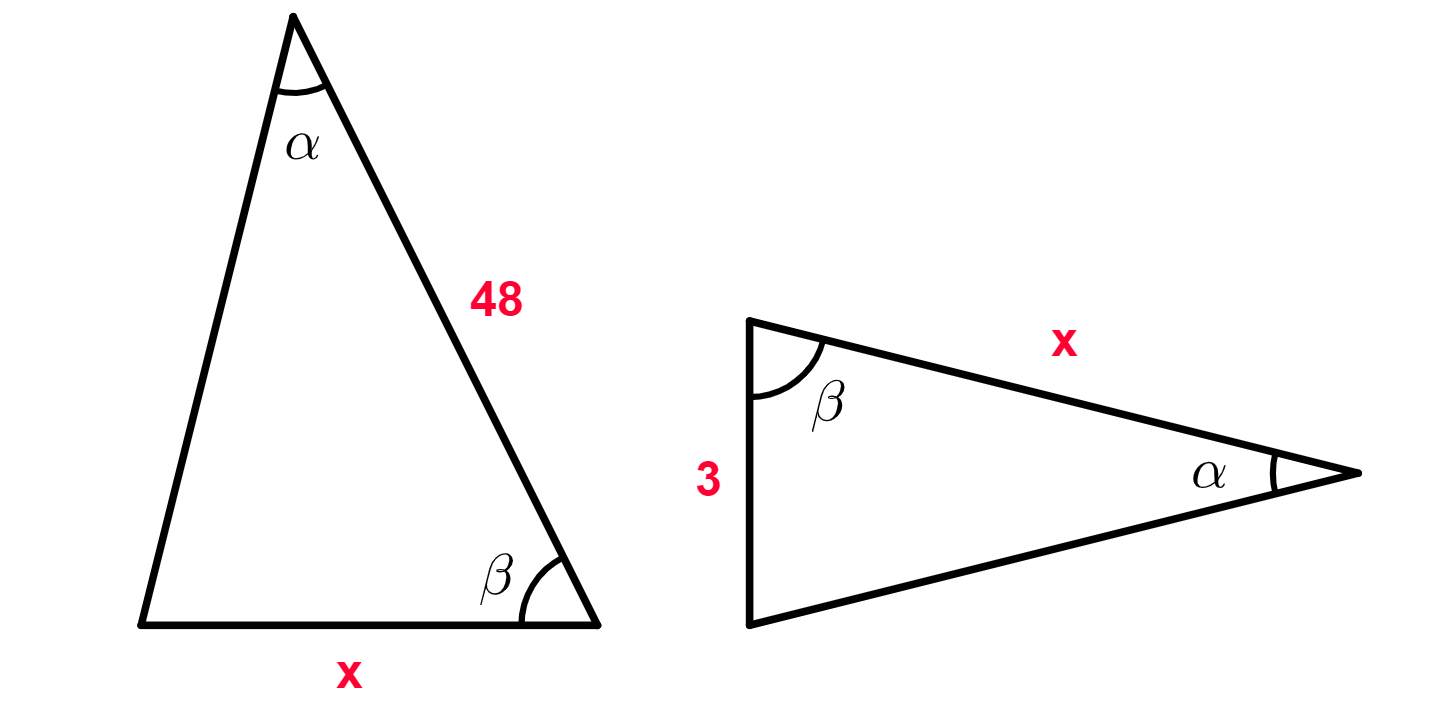
Questão 2. Determine o valor de x na figura abaixo:
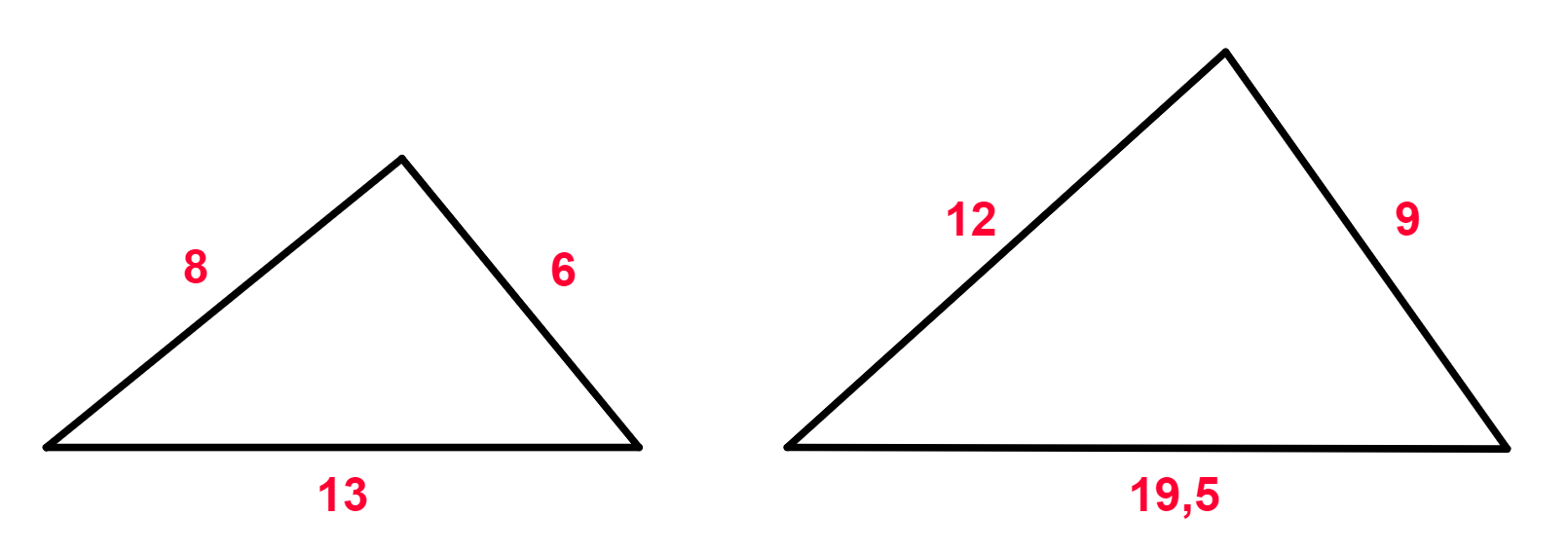
Questão 3. Verifique se os triângulos abaixo são semelhantes:
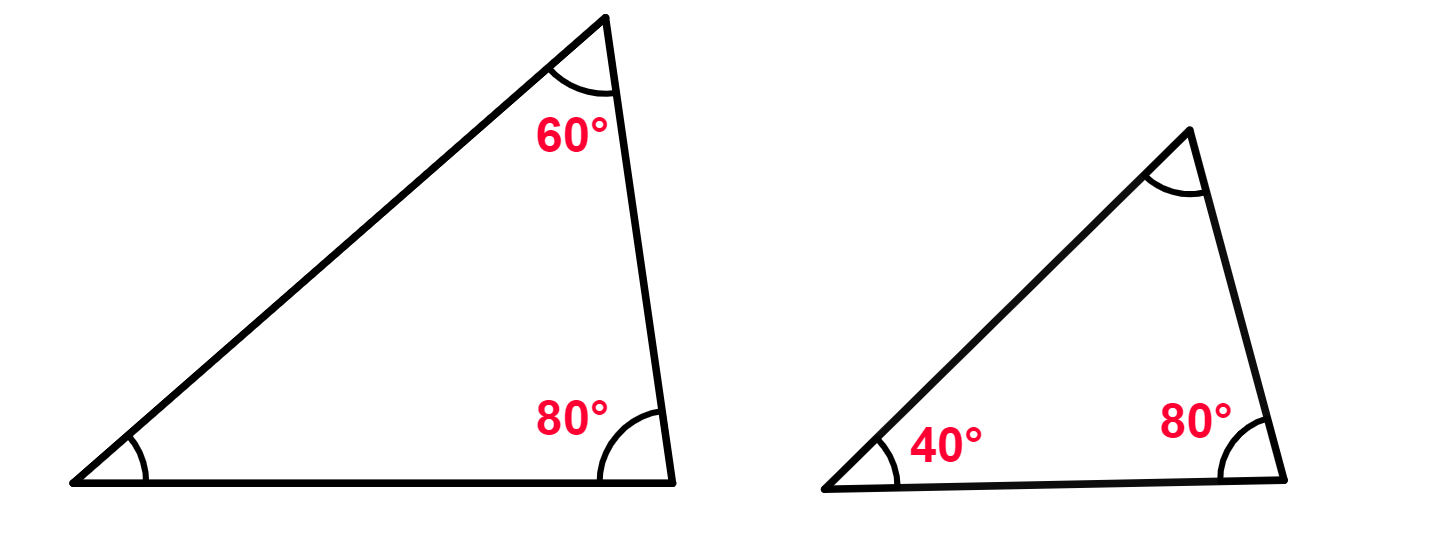
Questão 4. Determine se os triângulos abaixo são semelhantes:
Questão 5. Verifique se os triângulos abaixo são semelhantes:
Questão 6. Sabendo que os segmentos e
são paralelos, determine a medida de
.
Resolução da questão 1
Como os triângulos ABC e OPQ possuem dois ângulos correspondentes de mesma medida, então, os triângulos são semelhantes.
Pela semelhança entre os triângulos, temos que:
Resolução da questão 2
Os triângulos possuem dois ângulos correspondentes de mesma medida, então, são semelhantes.
Pela semelhança entre os triângulos, temos que:
Resolução da questão 3
Vamos verificar se os lados dos triângulos são proporcionais:
Lado 1:
Lado 2:
Lado 3:
Então, os triângulos são semelhantes e a razão de proporção é 2/3.
Resolução da questão 4
Devemos nos lembrar que a soma dos ângulos internos de um triângulo é igual a 180°. Dessa forma, podemos descobrir o valor do ângulo desconhecido em cada triângulo.
Triângulo maior:
180° – 80° – 60° = 40°
→ Os três ângulos desse triângulo são: 80°, 60° e 40°.
Triângulo menor:
180° – 80° – 40° = 60°
→ Os três ângulos desse triângulo são: 80°, 40° e 60°.
Então, os dois triângulos possuem dois ângulos correspondentes de mesma medida, portanto, são semelhantes.
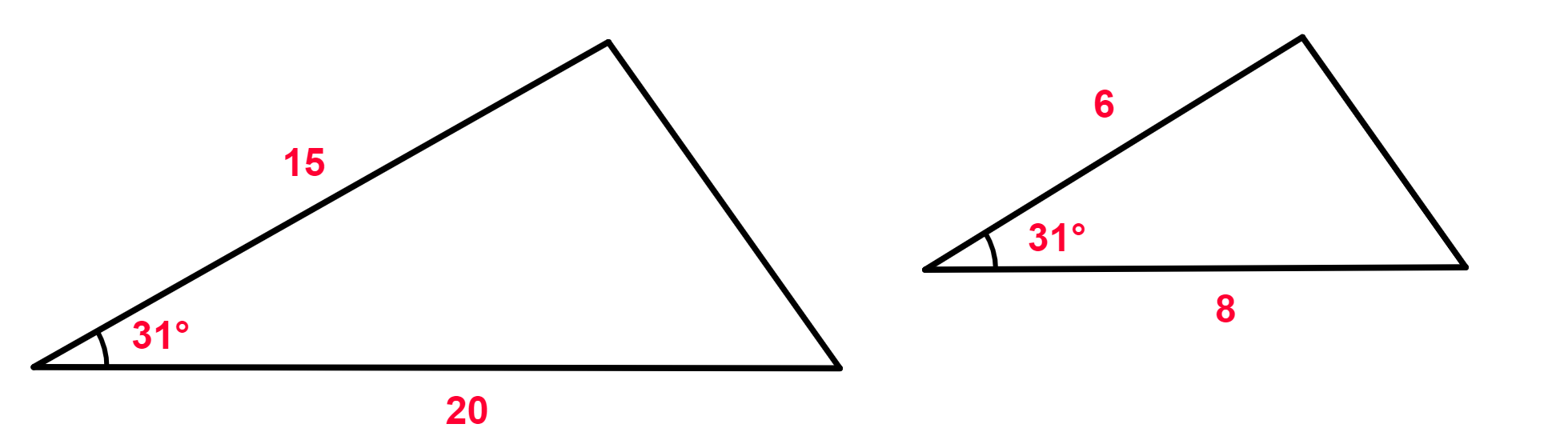
Resolução da questão 5
Vamos verificar se os lados são proporcionais:
Lado 1:
Lado 2:
Logo, os triângulos possuem dois lados proporcionais, com razão de proporção igual a 5/2. Além disso, o ângulo entre esses lados tem a mesma medida, 31°.
Portanto, os triângulos são semelhantes.
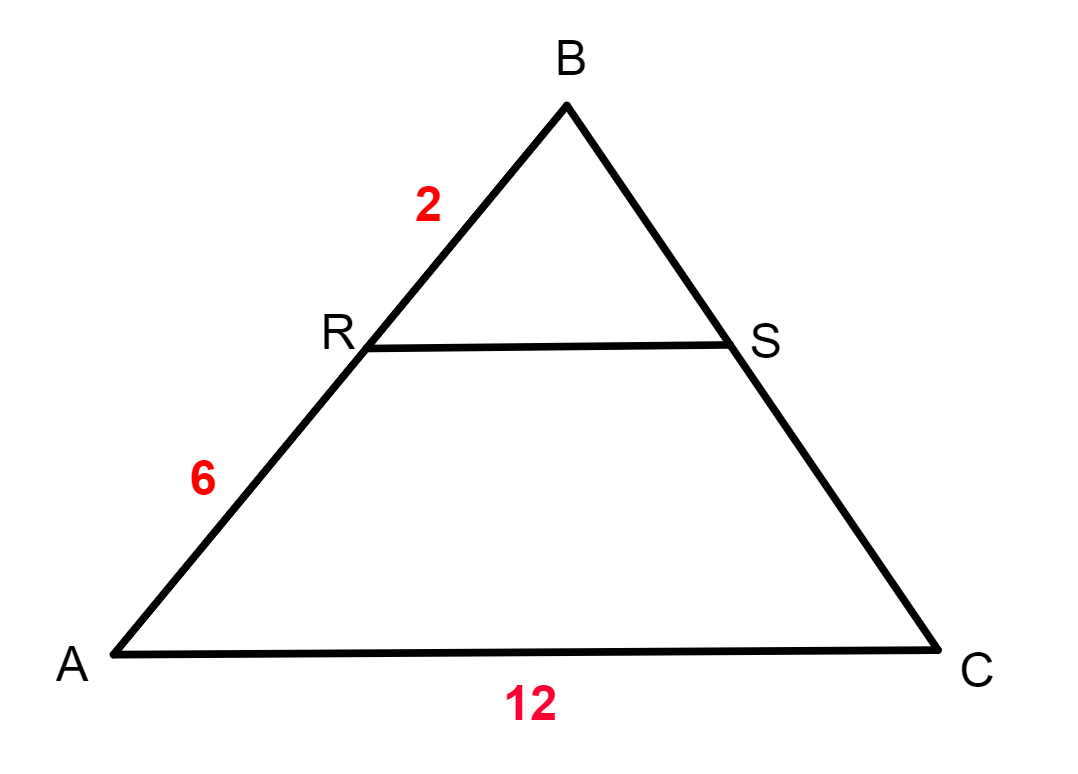
Resolução da questão 6
Como os segmentos e
são paralelos, então, os triângulos RBS e ABC são semelhantes.
Pela semelhança dos triângulos, temos que:
Você também pode se interessar:
- Área do Triângulo
- Classificação dos triângulos
- Congruência de triângulos
- Relações métricas no triângulo retângulo

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.