Tangência à circunferência

Saiba como verificar se existem ou não retas tangentes a uma circunferência dado um ponto e como determinar a equação dessas retas.

Por Elainy Marciano Publicado em 30/11/2020 - 17:28

Dado um ponto e uma circunferência em um plano, podemos determinar se existem ou não retas que passam por esse ponto e que são tangentes à circunferência.

Entenda mais sobre tangência à circunferência.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Retas tangentes à circunferência passando por um ponto

Temos três casos possíveis em relação à existência de retas tangentes à circunferência dado um ponto.

Se o ponto P estiver no interior da circunferência, não há nenhuma reta tangente à circunferência que passe por ele.
Se o ponto P for um ponto da circunferência, há uma única reta tangente à circunferência que passe por ele.
Se o ponto P estiver no exterior da circunferência, há duas retas tangentes à circunferência que passe por ele.

Posição relativa de um ponto a uma circunferência

Para saber a posição relativa de um ponto em relação a uma circunferência, basta observar a distância do centro da circunferência até o ponto e comparar com o valor do raio da circunferência.

Se a distância do centro C ao ponto P é menor que o raio ⇒ Ponto P é interno ⇒ Nenhuma reta tangente.
Se a distância do centro C ao ponto P é igual ao raio ⇒ Ponto P pertence à circunferência ⇒ Apenas uma reta tangente.
Se a distância do centro C ao ponto P é maior que o raio ⇒ Ponto P é externo ⇒ Duas retas tangentes.

Como determinar a reta tangente a uma circunferência?

Para determinar a equação da reta tangente a uma circunferência passando por um ponto, a primeira coisa a ser feita, é verificar a posição relativa do ponto, para saber se não há nenhuma, uma ou duas retas tangentes.

Em seguida, determinamos a equação reduzida da reta que passa pelo ponto $\dpi{120} \mathrm{P(x_0,y_0)}$ e cujo coeficiente angular é $\dpi{120} \mathrm{m}$ .

$\dpi{120} \mathrm{y - y_0 = m(x-x_0)}$

O ponto P já conhecemos, mas e o coeficiente angular, como podemos calcular?

Uma das formas, é utilizar a fórmula da distância do centro $\dpi{120} \mathrm{C(x_c, y_c)}$ da circunferência até a reta tangente t:

$\dpi{120} \mathrm{d_{C,t} = \frac{ax_c+by_c+c}{\sqrt{a^2 + b^2}}}$

Exemplo

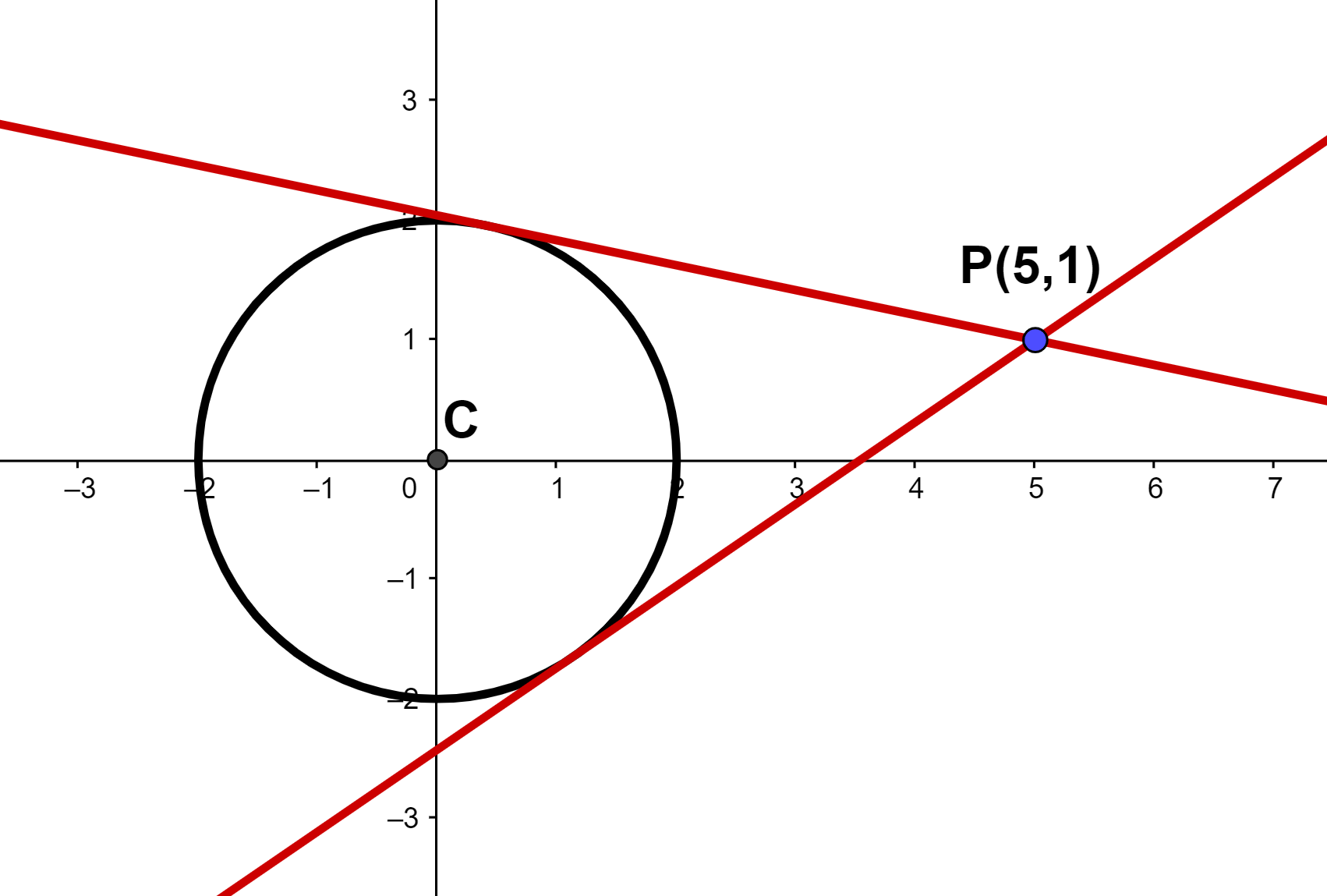
Determine a equação da reta tangente à circunferência $\dpi{120} \mathbf{y^2 + x^2 = 4}$ e que passa pelo ponto P(5,1).

Veja que na circunferência, temos centro C(0,0) e r = √4 = 2.

A primeira coisa que vamos fazer é verificar a posição relativa do ponto P à circunferência, usando a fórmula da distância entre dois pontos:

$\dpi{120} \mathrm{d_{C, P}} = \sqrt{(0 - 5)^2 +(0-1)^2} = \sqrt{25 + 1} = \sqrt{26}\approx 5,09$

Como r = 2, então, $\dpi{120} \mathrm{d_{C,P}> r}$ , o que significa que o ponto é externo à circunferência e existem duas retas tangentes à circunferência passando pelo ponto P.

Substituindo o ponto P(5,1) na equação reduzida da reta, temos que a equação das retas tangentes é:

$\dpi{120} \mathrm{y - 1 = m(x-5)}$

Fazendo algumas manipulações simples, obtemos a equação geral (ax + by + c = 0) das retas tangentes:

$\dpi{120} \mathrm{ m x - y - 5m + 1 = 0 }$

Sendo a = m, b = -1 e c = -5m + 1.

A diferença entre essas duas retas tangentes é dada pelo valor do coeficiente angular m. Vamos utilizar a fórmula da distância entre o centro C e a reta tangente, para determinar m.

$\dpi{120} \mathrm{d_{C,t} = \frac{ax_c+by_c+c}{\sqrt{a^2 + b^2}}}$

$\dpi{120} \Rightarrow \mathrm{d_{C,t} = \frac{mx_c-1y_c - 5m +1}{\sqrt{m^2 + 1}}}$

Sendo C(0,0), temos:

$\dpi{120} \Rightarrow \mathrm{d_{C,t} = \frac{m.0-1.0 - 5m +1}{\sqrt{m^2 + 1}}}$

$\dpi{120} \Rightarrow \mathrm{d_{C,t} = \frac{- 5m +1}{\sqrt{m^2 + 1}}}$

Como a distância do centro da circunferência até a reta tangente (qualquer uma delas) é igual ao raio da circunferência, ou seja, $\dpi{120} \mathrm{d_{C,t} =2}$ , temos que:

$\dpi{120} \Rightarrow \mathrm{\frac{- 5m +1}{\sqrt{m^2 + 1} }=2}$

Resolvendo essa equação, podemos determinar o valor de m:

$\dpi{120} \mathrm{- 5m + 1 = 2.\sqrt{m^2 + 1}}$

$\dpi{120} \Rightarrow \mathrm{(- 5m + 1)^2 = 4.(m^2 + 1)}$

$\dpi{120} \Rightarrow \mathrm{25m^2 -10m + 1 = 4m^2 + 4}$

$\dpi{120} \Rightarrow \mathrm{21m^2 -10m - 3 = 0}$

Essa última equação é uma equação do 2º grau, suas raízes podem ser determinadas pela fórmula de Bhaskara:

$\dpi{120} \mathrm{m' \approx 0,68}$

$\dpi{120} \mathrm{{m}'' \approx -0,20}$

Portanto, esses são os coeficientes angulares das retas tangentes à circunferência. Basta substituir esses valores na equação: $\dpi{120} \mathrm{ m x - y - 5m + 1 = 0 }$ .

$\dpi{120} \mathrm{m = 0,68}$ :