Cálculo do coeficiente angular
Aprenda a calcular o coeficiente angular de três formas diferentes: a partir do ângulo, de dois pontos e da equação da reta.
O coeficiente angular de uma reta é um valor que indica a inclinação da reta em relação ao eixo das abscissas (eixo x).
Existem algumas formas diferentes de calcular o coeficiente angular, vamos ver quais são?
Cálculo do coeficiente angular
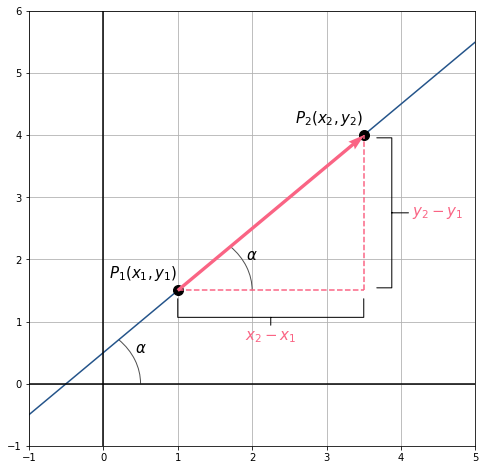
Considere, por exemplo, a reta da figura abaixo:
O coeficiente angular corresponde à tangente do ângulo . Assim, representando o coeficiente angular pela letra
, temos que:
E podemos estabelecer algumas formas diferentes de calcular o coeficiente angular.
Cálculo do coeficiente angular a partir do ângulo
Sabendo o ângulo de inclinação, basta calcular a tangente desse ângulo.
Exemplo: se , então:
Para saber o valor da tangente de um ângulo, basta consultar uma tabela trigonométrica.
Cálculo do coeficiente angular a partir de dois pontos
Se conhecemos dois pontos que pertencem à reta, e
, podemos calcular o coeficiente angular da seguinte forma:
Para entender essa fórmula, observe que na figura, forma -se um triângulo retângulo, com e
e lembre-se que
.
Exemplo: dados os pontos e
, temos:
Cálculo do coeficiente angular a partir da equação da reta
Considere a equação da reta , com a
e
números reais e
, então:
Exemplo: dada a equação , podemos reescrevê-la da seguinte forma:
Portanto, .
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.