Adição e subtração de matrizes

A adição ou subtração de matrizes é feita somando ou subtraindo os elementos de mesma posição nas matrizes. Assim, esse tipo de cálculo entre matrizes é bem simples de ser feito.

Contudo, devemos ficar atentos a ordem das matrizes, pois só podemos somar ou subtrair matrizes de mesma ordem.

Ordem de uma matriz

A ordem de uma matriz se refere ao número de linhas e ao número de colunas que ela possui. Por exemplo, a matriz A abaixo tem 2 linhas e 3 colunas:

Então, dizemos que a matriz A é de ordem 2 por 3, ou ainda, 2 x 3.

Soma de matrizes

Para fazer a soma de matrizes, basta somar os elementos de mesma posição. Mas existe uma condição para realizar essa operação: as matrizes devem possuir a mesma ordem.

Se tivermos A de ordem m por n e B, também de ordem m por n, o resultado da soma será uma matriz C de ordem m por n.

A (m x n) + B (m x n) = C (m x n)

Subtração de matrizes

De modo semelhante à adição, para fazer a subtração de duas matrizes, elas devem possuir a mesma ordem. Se essa condição for satisfeita, basta subtrair os elementos de mesma posição.

Considerando uma matriz A de ordem m por n e uma matriz B, também de ordem m por n, o resultado da subtração será uma matriz C de ordem m por n.

A (m x n) – B (m x n) = C (m x n)

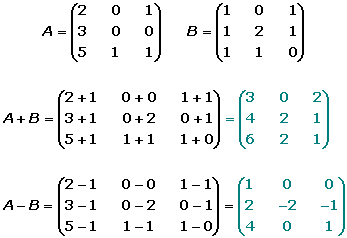
Exemplo – Adição e subtração de matrizes

Considerando uma matriz A de ordem 3 x 3 e uma matriz B de ordem 3 x 3, vamos calcular a soma, A + B, e a subtração A – B.

Observe que a matriz resultante, tanto na soma como na subtração, possui a mesma ordem que as matrizes A e B, ou seja, 3 x 3.

Propriedades da adição de matrizes

Considerando três matrizes A, B e C de ordem m por n, temos as seguintes propriedades:

• Comutativa: A + B = B + A
• Associativa: (A + B) + C = A + (B + C)
• Elemento neutro: A + 0 = 0 + A = A
• Elemento oposto: A + (-A) = (-A) + A = 0

Onde 0 é uma matriz nula de ordem m por n.

Você também pode se interessar:

• Tipos de matrizes
• Multiplicação de matrizes
• Determinante de uma matriz