Agrupamento de dados em intervalos

O agrupamento de dados em intervalos é utilizado para obter a distribuição de frequência de dados contínuos ou com muitas observações.

Por Elainy Marciano Publicado em 15/10/2020 - 17:55

O agrupamento de dados em intervalos é utilizado para obter a distribuição de frequência em conjuntos de dados contínuos ou com muitas observações, ainda que sejam valores discretos.

Distribuição de frequências

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

A partir da análise de dados é possível extrair informações e obter insights para a tomada de decisões importantes, no meio acadêmico e corporativo.

Contudo, os dados brutos dizem pouco ou quase nada sobre o comportamento de uma variável, tornando necessário o uso de técnicas para organizar e resumir os dados, como a distribuição de frequências.

Quando contamos quantas vezes um valor aparece em um conjunto de dados, estamos obtendo a sua frequência absoluta.

Ao calcular as frequência de cada um dos possíveis valores de uma variável, obtemos a distribuição de frequências.

Dividindo a frequência absoluta pelo total de observações, podemos obter, ainda, a frequência relativa.

Exemplo:

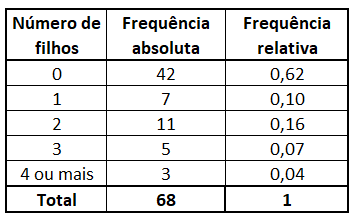
Distribuição de frequências do número de filhos dos funcionários de uma empresa.

Dados agrupados em intervalos

Quando um conjunto de dados apresenta muitas observações ou os dados são contínuos, eles devem ser agrupados em intervalos e as frequências são obtidas para cada intervalo, também chamado de classe.

Veja os passos para obter o agrupamento de dados.

1º passo) Definir o número de classes.

Não existe uma regra para a quantidade de classes.

Contudo, se forem consideradas muitas classes, os dados não serão resumidos, teremos uma tabela muito extensa. Por outro lado, se forem consideradas poucas classes, perderemos informação sobre os dados, teremos uma tabela muito reduzida.

Assim, o ideal é determinar o número de classes com base na natureza dos dados e no conhecimento que se tenha sobre eles.

2º passo) Calcular a amplitude das classes.

Para calcular a amplitude das classes, precisamos do número de classes e da amplitude total.

$\dpi{120} Amplitude \, das \, classes = \frac{Amplitude \, total}{n^{\circ} \, de \, classes}$

Sendo que:

$\dpi{120} Amplitude\, total = Maior \, valor - menor\, valor$

3º passo) Calcular os limites das classes.

As classes são formadas pelo limite inferior (Li) e limite superior (Ls) e podem ser expressas da seguinte forma:

$\dpi{120} \mathrm{Li\vdash ls}$

Que indica que o intervalo contém os valores maiores ou iguais a Li e menores que Ls, ou seja, é o intervalo [Li, Ls).

A primeira classe começa com Li sendo o menor valor dos dados. Para obter Ls, somamos Li a amplitude das classes.

As demais classes são obtidas de forma semelhante, considerando Li como o valor Ls da classe anterior.

Exemplo:

Considere as alturas, em cm, de 25 estudantes de educação física, em ordem crescente.

159 160 164 168 169 169 169 170 172 172 173 175 175 175 177 179 180 182 182 184 186 186 188 190 192

Vamos considerar 5 classes.

$\dpi{120} Amplitude\, total = 192 - 159 = 33$

$\dpi{120} Amplitude \, das \, classes = \frac{33}{5} = 6,6$

Primeira classe:
Li = 159 e Ls = 159 + 6,6 = 165,6

Segunda classe:
Li = 165,6 e Ls = 165,6 + 6,6 = 172,2

Terceira classe:
Li = 172,2 e Ls = 172,2 + 6,6 = 178,8

Quarta classe:
Li = 178,8 e Ls = 178,8 + 6,6 = 185,4

Quinta classe:
Li = 185,4 e Ls = 185,4 + 6,6 = 192

Distribuição de frequências das alturas dos 25 estudantes de Educação Física:

Classes de alturas (cm)	Frequência absoluta	Frequência relativa
$\dpi{120} 159\vdash 165,6$	3	0,12
$\dpi{120} 165,6\vdash 172,2$	7	0,28
$\dpi{120} 172,2\vdash 178,8$	5	0,2
$\dpi{120} 178,8\vdash 185,4$	5	0,2
$\dpi{120} 185,4\vdash 192$	5	0,2
Total	25	1

Observação: na última classe, o limite superior pertence à classe.

Você também pode se interessar:

Estatística