Ângulo entre dois vetores

O ângulo entre vetores pode ser calculado a partir do produto interno entre eles e suas normas. Veja a fórmula!

Por Elainy Marciano Publicado em 03/11/2020 - 18:19

Em matemática ou física, os vetores são segmentos de reta com direção, sentido e comprimento, que são utilizados para representar grandezas como força, velocidade e aceleração.

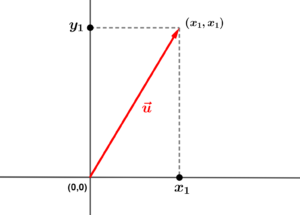
Vetores indicam trajetórias e podem ser definidos através de um sistema de coordenadas (x, y). Considerando como origem do segmento o ponto (0,0), na figura abaixo está representado um vetor $\dpi{120} \boldsymbol{\vec{u}}$ cuja extremidade é o ponto $\dpi{120} \boldsymbol{ $x_1, y_1$}$ .

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Notação: $\dpi{120} \boldsymbol{\vec{u}= $x_1, y_1$}$ .

A ordenada $\dpi{120} \boldsymbol{x_1}$ é chamada de componente horizontal e a abscissa $\dpi{120} \boldsymbol{y_1}$ , de componente vertical.

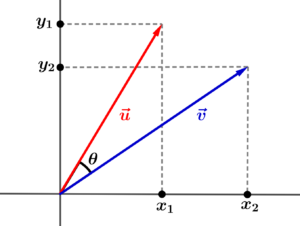
Agora, considere, além do vetor $\dpi{120} \boldsymbol{\vec{u}= $x_1, y_1$}$ , outro vetor $\dpi{120} \boldsymbol{\vec{v}= $x_2, y_2$}$ e um ângulo formado entre eles, conforme é apresentado na figura abaixo.

Esse ângulo entre os vetores pode ser calculado por uma fórmula que envolve o produto interno entre os vetores e a norma (comprimento) de cada vetor.

Ângulo entre dois vetores

Dados dois vetores $\dpi{120} \boldsymbol{\vec{u}= $x_1, y_1$}$ e $\dpi{120} \boldsymbol{\vec{v}= $x_2, y_2$}$ , o cosseno do ângulo $\dpi{120} \boldsymbol{\theta}$ entre eles está relacionado com produto interno entre os vetores e suas normas da seguinte forma:

$\dpi{120} \boldsymbol{cos\, \theta = \frac{\left \langle \vec{u}, \vec{v} \right \rangle}{\|\vec{u} \|.\|\vec{v} \| }}$

O numerador da fração é o produto interno entre os vetores, dado por:

$\dpi{120} \boldsymbol{\left \langle \vec{u}, \vec{v} \, \right \rangle = x_1\cdot x_2+y_1\cdot y_2}$

E o denominador é o produto entre as normas de cada um dos vetores, sendo que:

$\dpi{120} \boldsymbol{\|\vec{u}\|= \sqrt{(x_1)^2+ (y_1)^2}}$

$\dpi{120} \boldsymbol{\|\vec{v}\|= \sqrt{(x_2)^2+ (y_2)^2}}$

Fazendo a substituição, verificamos que a fórmula do ângulo entre dois vetores é:

$\dpi{120} \boldsymbol{cos\, \theta = \frac{x_1\cdot x_2+y_1\cdot y_2}{\sqrt{(x_1)^2+(y_1)^2} \cdot \sqrt{(x_2)^2+(y_2)^2}}}$

Exemplo:

Calcule o ângulo entre os vetores $\dpi{120} \boldsymbol{\vec{u}= $2,4$}$ e $\dpi{120} \boldsymbol{\vec{v}= $5,3$}$ .

Aplicando os valores na fórmula, temos que:

$\dpi{120} \boldsymbol{cos\, \theta = \frac{2\cdot 5+4\cdot 3}{\sqrt{(2)^2+(4)^2} \cdot \sqrt{(5)^2+(3)^2}}}$

$\dpi{120} \Rightarrow \boldsymbol{cos\, \theta = \frac{10+12}{\sqrt{4+16} \cdot \sqrt{25+9}}}$

$\dpi{120} \Rightarrow \boldsymbol{cos\, \theta = \frac{22}{\sqrt{20} \cdot \sqrt{34}}}$

$\dpi{120} \Rightarrow \boldsymbol{\theta = cos^{-1}\left (\frac{22}{\sqrt{20} \cdot \sqrt{34}} \right ) }$

Utilizando uma calculadora ou uma tabela trigonométrica, podemos ver que:

$\dpi{120} \boldsymbol{ \theta = 32,47^{\circ}}$

Você também pode se interessar:

Geometria analítica