Círculo trigonométrico
Círculo trigonométrico é essencial em trigonometria. Saiba o que é, como utilizar, quais os quadrantes, sinais, ângulos, radianos e razões trigonométricas.
O círculo trigonométrico é um círculo utilizado para representação de ângulos e radianos, sendo essencial em estudos de trigonometria.
O raio do círculo trigonométrico é igual a 1 e, normalmente, o centro é o ponto (0,0) do plano cartesiano.
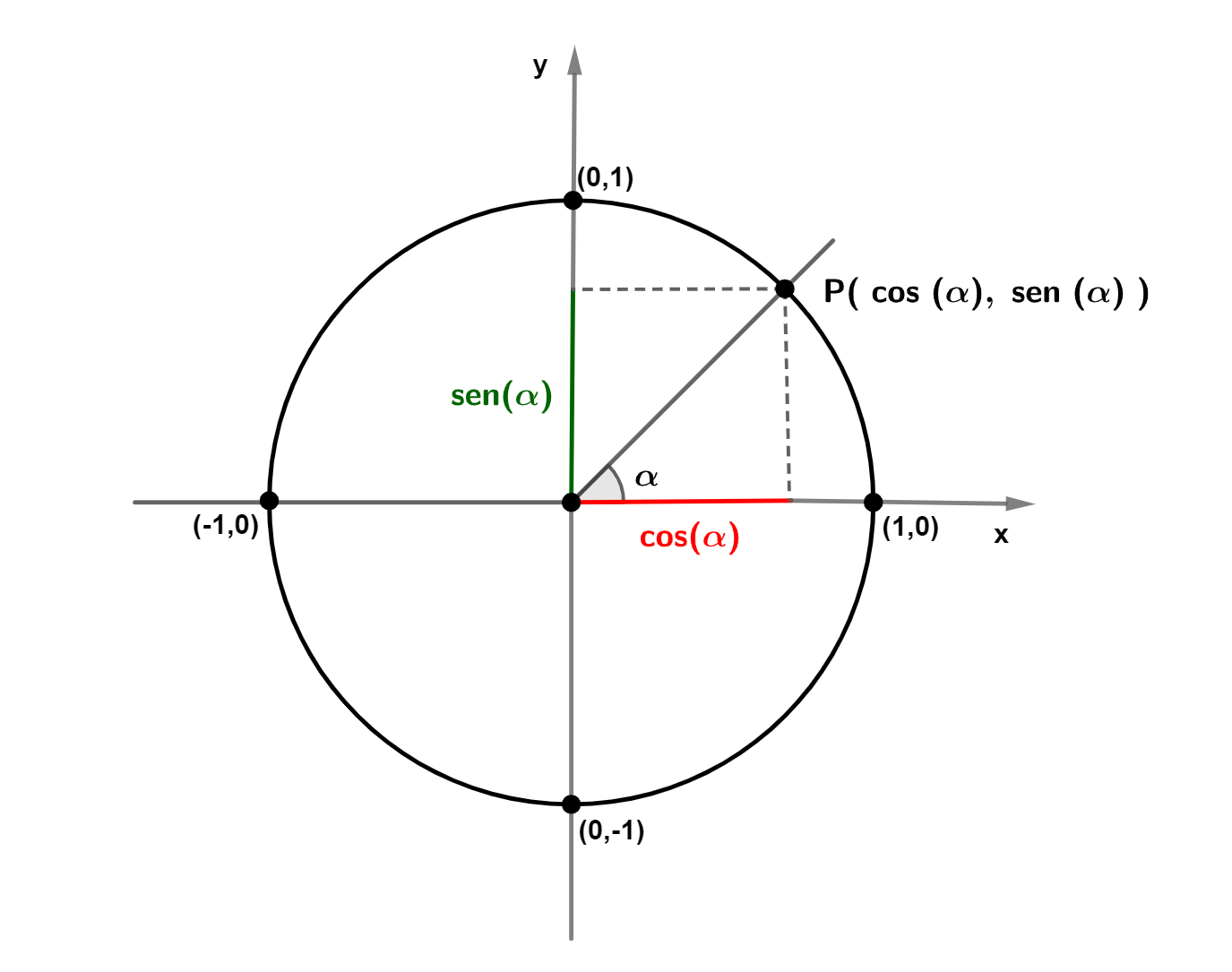
Cada ponto P da circunferência do círculo trigonométrico está associado a um ângulo . A primeira coordenada do ponto corresponde ao cosseno de
e a segunda coordenada, ao seno de
.
P(x, y) = P(cos (), sen (
))
Dessa forma, o eixo x é chamado de eixo dos cossenos e o eixo y de eixo dos senos.
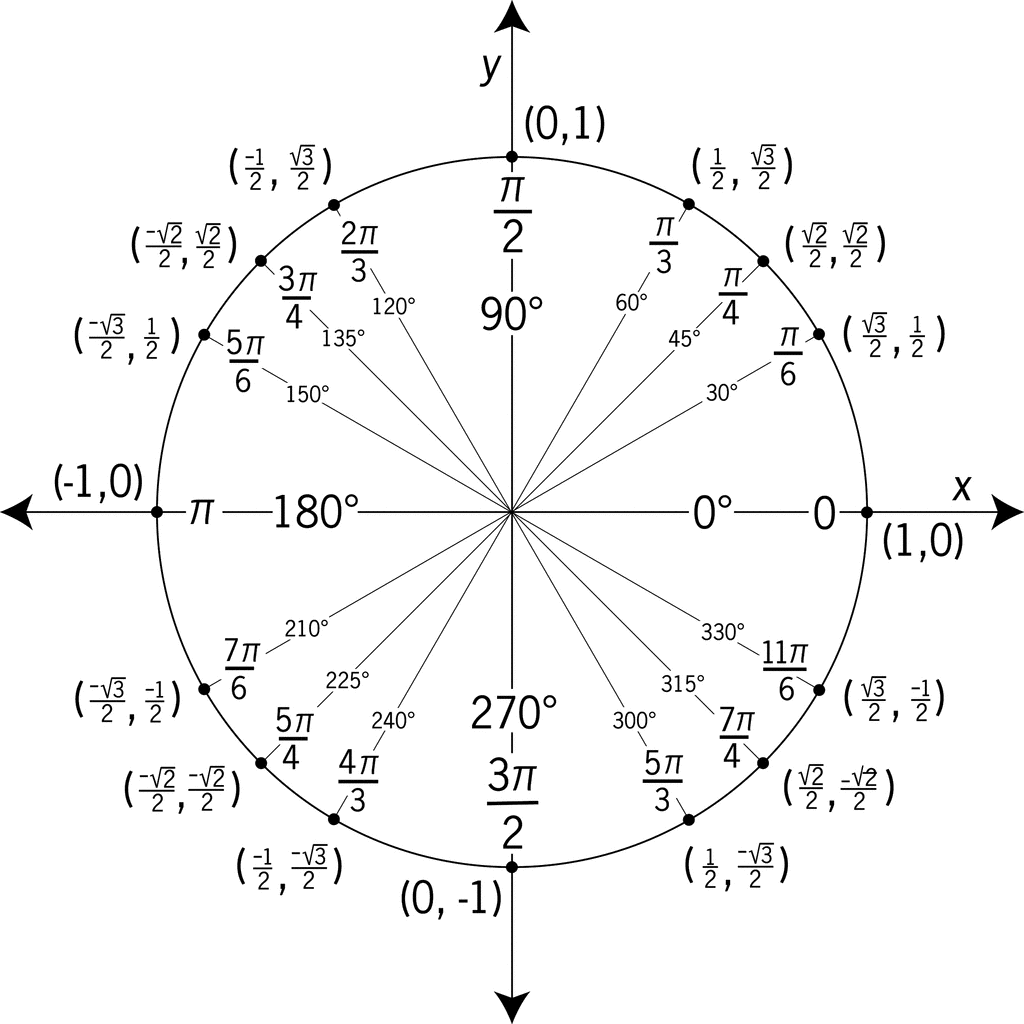
Ângulos notáveis no círculo trigonométrico
Os ângulos mais utilizados são chamados de ângulos notáveis, os principais são 30°, 45° e 60°.
Vamos tomar como exemplo o ângulo de 30°. No círculo trigonométrico, esse ângulo está associado ao ponto P(cos (30°), sen (30°)).
Então, só resta saber qual o valor das funções trigonométricas para esses ângulos. As principais funções são seno, cosseno e tangente:

Mas, além desses, podem ser considerados notáveis, os ângulos de 0° e 90°.
Se considerarmos um ângulo de 0°, teremos o ponto P(cos (0°), sen (0°)) = P (0,1) e se considerarmos um ângulo de 90°, o ponto P(cos (90°), sen (90°)) = P (1,0).
De onde temos que:
- seno de 0° = cosseno de 90° = 1
- seno de 90° = cosseno de 0° = 0
E quanto aos demais ângulos, os seus valores podem ser consultados em uma tabela trigonométrica.
Ângulos e radianos no círculo trigonométrico
A medida de um ângulo pode ser apresentada em graus ou em radianos no círculo trigonométrico.
Uma volta completa no círculo corresponde a 360° ou em radianos. O valor de
, nesse caso, é igual a 180°.
Então, por exemplo, 30° é o mesmo que , pois
.
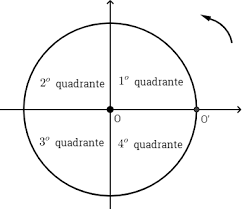
Quadrantes do círculo trigonométrico
Um círculo trigonométrico pode ser repartido em quatro partes iguais, que são chamadas de quadrantes.
- 1º quadrante: de 0° a 90° (0 a
)
- 2º quadrante: de 90° a 180° (
)
- 3º quadrante: de 180° a 270° (
)
- 4º quadrante: de 270° a 360° (
)
Para saber o quadrante de um ângulo maior que 360°, é necessário saber qual o seu corresponde de 0° a 360°.
Exemplo: ângulo de 415°.
Dividindo 415° por 360°, o quociente é 1 e o resto é 55°. Isso significa que 415° corresponde a uma volta inteira do círculo e mais 55°.
Como 55° está no 1° quadrante, então, a extremidade do ângulo 415° pertence ao 1° quadrante.
Sinal das funções no círculo trigonométrico
Os valores das funções trigonométricas podem ser negativos ou positivos. O sinal das funções pode ser representado no círculo trigonométrico conforme os quadrantes.
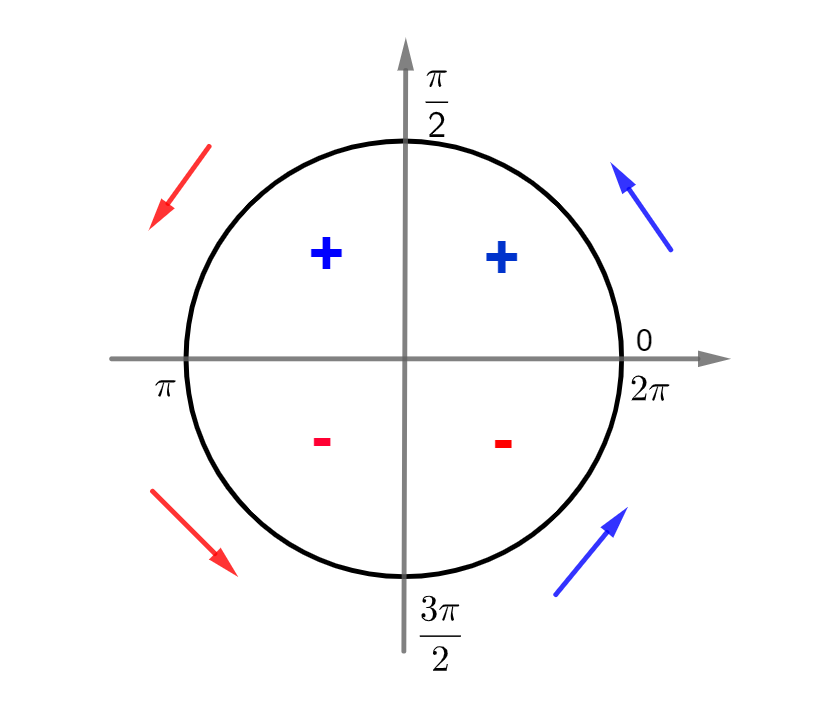
Função seno:
Sinal da função:
- Positiva (+) de 0 a
- Negativa (–) de
a 2
Comportamento da função:
- Crescente (⇑) de 0 a
- Decrescente de (⇓) de
a
- Crescente (⇑) de
a 2
Função cosseno:
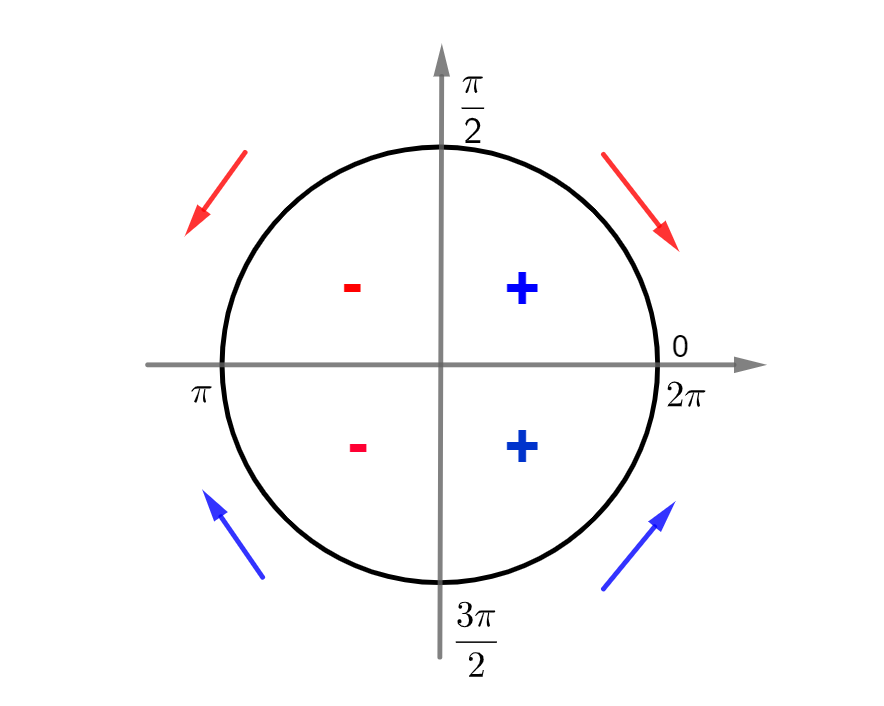
Sinal da função:
- Positiva (+) de 0 a
- Negativa (–) de
a
- Positiva (+) de
a 2
Comportamento da função:
- Decrescente de (⇓) de 0 a
- Crescente (⇑) de
a 2
Função tangente:
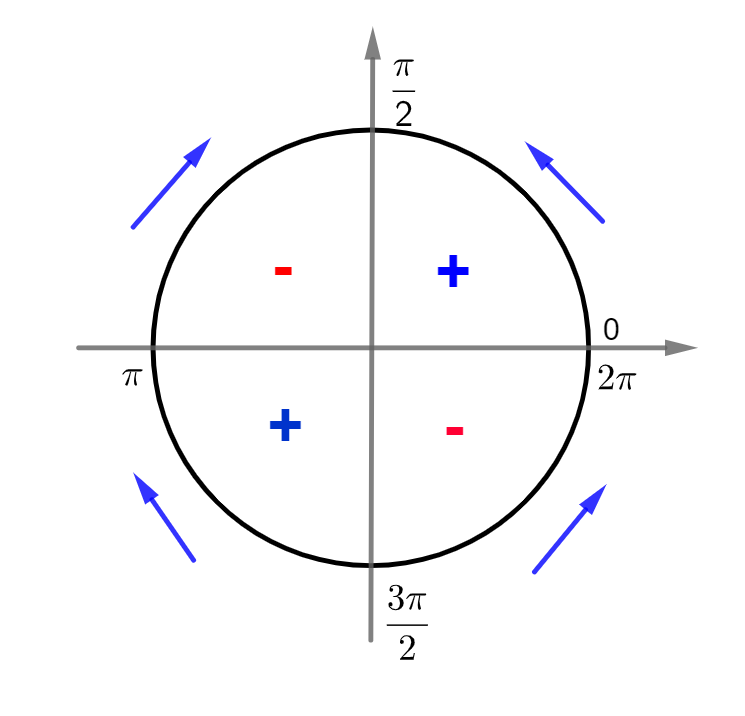
Sinal da função:
- Positiva (+) de 0 a
- Negativa (–) de
a
- Positiva (+) de
a
- Negativa (–) de
a 2
Comportamento da função:
- Crescente (⇑) de 0 a 2
Razões trigonométricas
As razões trigonométricas são utilizadas para determinar medidas de ângulos e lados desconhecidos em triângulos retângulos.
As principais razões trigonométricas são:
Você também pode se interessar:
- Lei dos senos
- Lei dos cossenos
- Relações métricas no triângulo retângulo
- Teorema de Pitágoras – História, fórmula, Triângulo Pitagórico

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.