Área da coroa circular

A coroa circular é uma região formada entre duas circunferências. Entenda mais sobre isso e veja a fórmula para calcular sua área.

Por Elainy Marciano Publicado em 29/10/2020 - 17:38

A coroa circular é uma região do plano formada a partir de duas circunferências de mesmo centro, mas raios diferentes, um maior e outro menor.

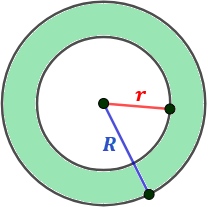
Na figura abaixo, uma circunferência de raio r é inscrita em uma circunferência de raio R, sendo R > r. Observe que o centro das duas circunferências é o mesmo.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

A coroa circular é a região colorida na figura e corresponde a diferença entre o círculo maior e o círculo menor.

Um exemplo de coroa circular no dia a dia é a borda de um relógio de parede com formato circular.

Área da coroa circular

A área da coroa circular pode ser obtida a partir da diferença entre a área do círculo maior, de raio R, e a área do círculo menor, de raio r.

Como calcular a área do círculo?

$\dpi{120} \mathrm{A_{Circulo\, maior} = \pi R^2}$

$\dpi{120} \mathrm{A_{Circulo\, menor} = \pi r^2}$

A diferença entre essas áreas é:

$\dpi{120} \mathrm{A_{Circulo\, maior} - A_{Circulo\, menor} = \pi R^2 - \pi r^2 = \pi(R^2-r^2) }$

Portanto, a fórmula da área da coroa circular é:

$\dpi{120} \mathbf{A_{Coroa \, circular} = \boldsymbol{\pi}(R^2-r^2) }$

Em que:

$\dpi{120} \boldsymbol{\pi\approx 3,14}$
R: raio do círculo maior;
r: raio do círculo menor.

Exemplo:

Calcular a área de uma coroa circular delimitada por duas circunferências de raio 5 e 3 metros.

Temos R = 5 e r = 3. Vamos aplicar na fórmula:

$\dpi{120} \mathrm{A_{Coroa \, circular} = 3,14\cdot (5^2-3^2) =50,24}$

Portanto, a área dessa coroa circular é igual a 50,24 m².

Você também pode se interessar:

Geometria plana

Elainy Marciano

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.