Bissetriz

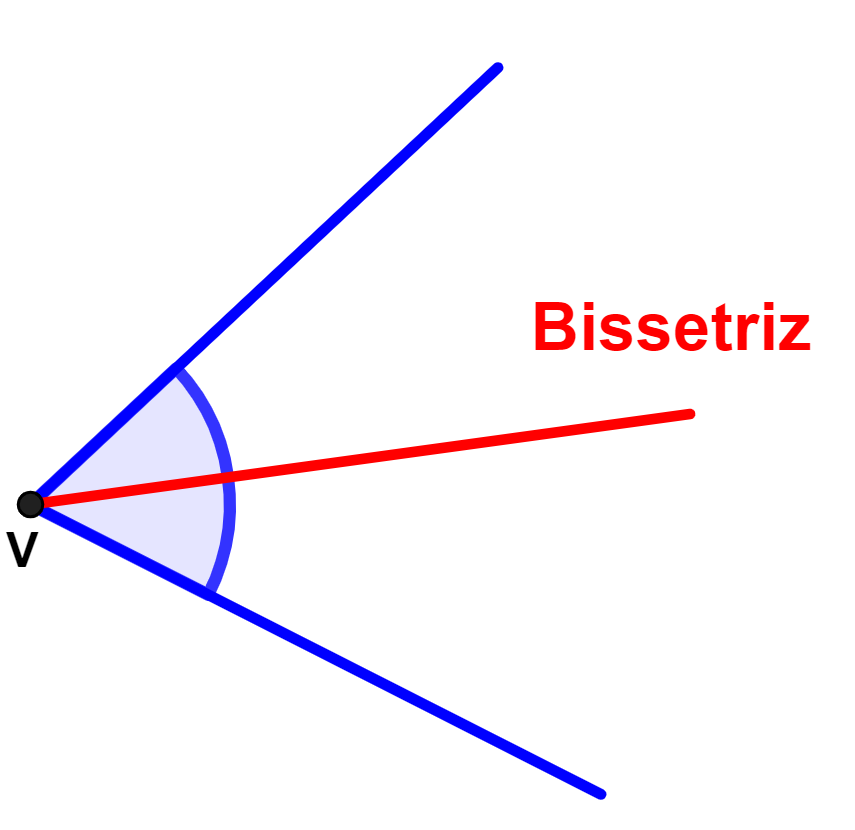
Bissetriz é uma semirreta com origem no vértice de um ângulo, que divide esse ângulo em dois ângulos de mesma medida.

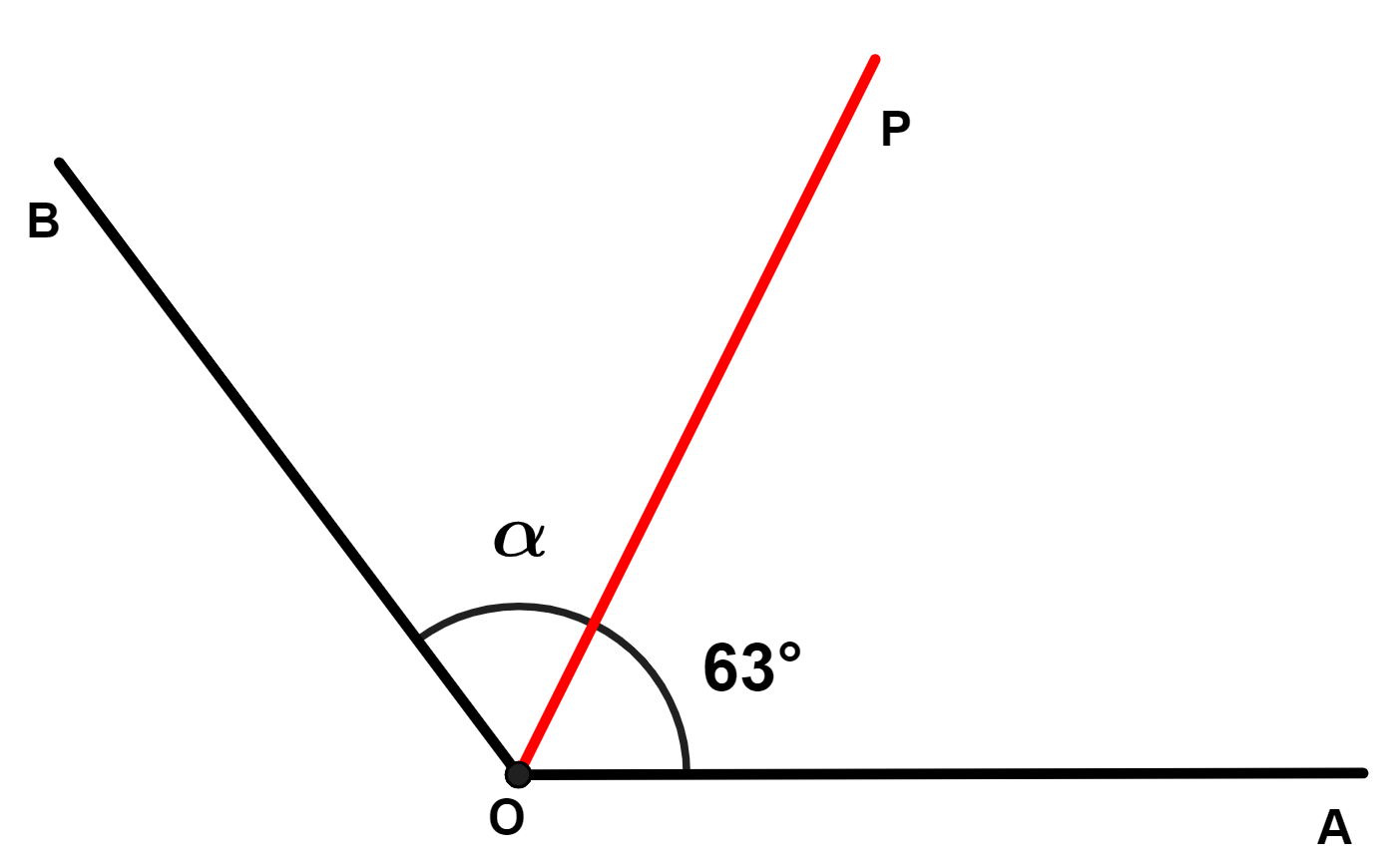
Exemplo: sabendo que a semirreta  é a bissetriz do ângulo AÔB, determine a medida do ângulo  na figura abaixo.

A bissetriz divide o ângulo em dois ângulos de mesma medida. Logo, o valor de  também é 63°.

Como encontrar a bissetriz

Há duas formas de traçar a bissetriz de um ângulo. Podemos usar o transferidor ou o compasso.

Bissetriz com o transferidor

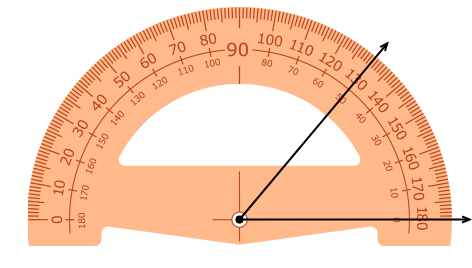
1º) Posicione o centro do transferidor sobre o vértice do ângulo, de forma que a escala correspondente ao zero (linha de fé) coincida com um dos lados do ângulo.

2º) Identifique a medida do ângulo e divida essa medida por 2 para saber a medida de cada ângulo formado pela bissetriz.

50° : 2 = 25°

3º) Posicione novamente o transferidor sobre o ângulo e marque um ponto no interior do ângulo indicando esse valor encontrado no passo 2.

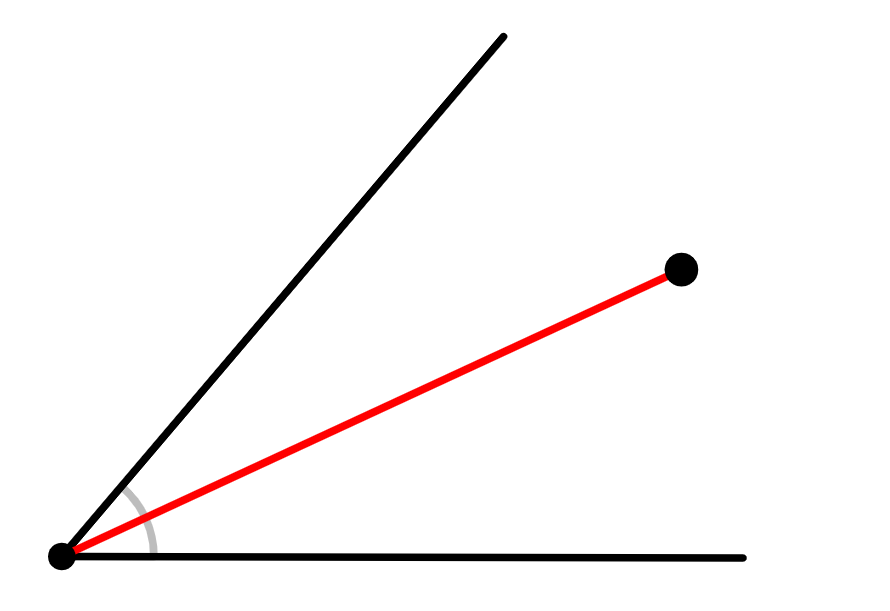
4º) Retire o transferidor e trace um segmento de reta que liga o vértice a esse ponto marcado.

Bissetriz com o compasso

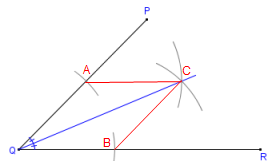
1º) Posicione a ponta seca do compasso no vértice do ângulo (Q) e trace um arco com uma abertura qualquer, marcando os pontos de cruzamento (A e B) do arco com as semirretas (P e R) que formam o ângulo.

2º) Sem mexer na abertura do compasso, posicione a ponta seca no ponto A e trace um arco. Em seguida, faça o mesmo no ponto B.

3º) Marque o ponto de intersecção (C) entre esses dois arcos traçados.

4º) Trace um segmento de reta que liga o vértice a esse ponto marcado.

Bissetriz de um triângulo

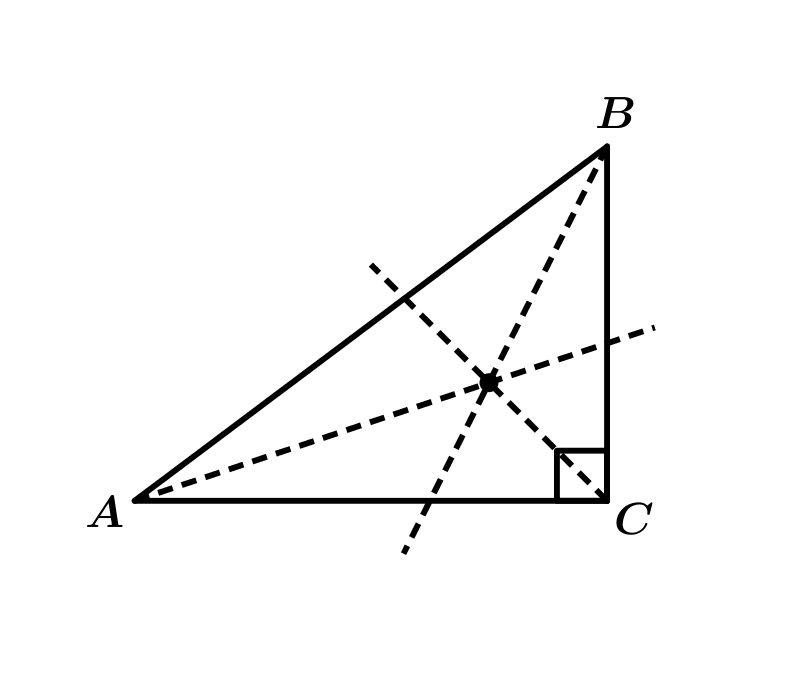
A bissetriz de cada ângulo interno de um triângulo é o segmento de reta que liga o vértice ao lado oposto, dividindo o ângulo em dois ângulos de mesma medida.

Como um triângulo possui três ângulos internos, é possível traçar segmentos de retas que são bissetrizes nesse triângulo.

Observe que os segmentos se cruzam em um ponto. Esse ponto é chamado de incentro.

Você também pode se interessar:

• Classificação dos triângulos
• Ângulos colaterais internos e externos
• Retas concorrentes
• Ângulos – Tipos, classificações e exemplos