Cilindro

Vários objetos têm a forma de um cilindro, por exemplo, uma latinha de refrigerante. Por isso, entenda como ele é formado, quais são seus componentes e como calcular as áreas e o volume.

Por Elainy Marciano Publicado em 13/02/2020 - 16:02

O cilindro é uma figura geométrica espacial, de corpo redondo e alongado. Ele é formado por dois círculos, um superior e um inferior, que são paralelos, de mesmo tamanho e estão em planos diferentes.

Componentes do cilindro

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Os principais componentes de um cilindro são:

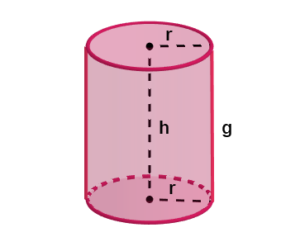
Base: É cada um dos círculos, superior e inferior;

Eixo: É a reta que passa pelo centro das bases;

Raio (r): É o raio das bases;

Altura (h): É a distância entre os planos das duas bases;

Geratriz (g): É cada um dos segmentos de reta que vão de uma base a outra.

Classificação do cilindro

Os cilindros podem ser classificados como cilindros retos e cilindros oblíquos.

Cilindro reto: Quando o eixo é perpendicular à base, formando um ângulo de 90º.

Cilindro oblíquo: Quando o eixo não é perpendicular à base.

Fórmulas do cilindro

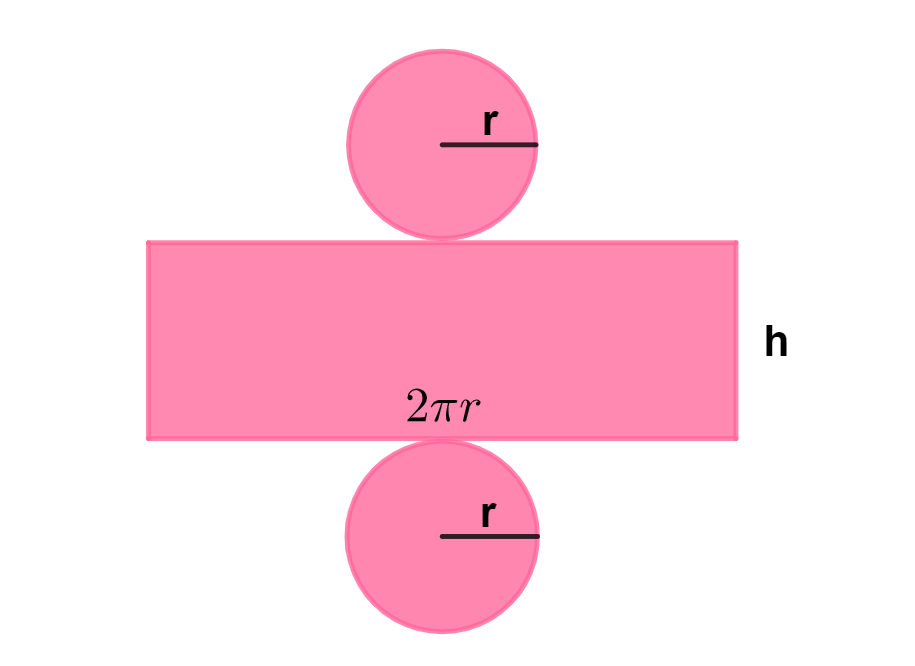
Na imagem a seguir, temos a planificação de um cilindro, que ajudará a compreender as fórmulas que serão apresentadas.

Área total (ou área externa) de um cilindro

A área total de um cilindro, ou área externa, é dada pela soma da área das bases mais a área da lateral, isto é,

$\dpi{120} \acute{A}rea\ total = {\color{Blue} \acute{A}rea \ das\ bases} + {\color{Magenta} \acute{A}rea\ da \ lateral}$

Área das bases

A área das bases de um cilindro é a área de um círculo de raio r. Como temos duas bases, multiplicamos por 2:

$\dpi{120} \acute{A}rea \ das \ bases = 2\cdot \pi r^2$

O valor aproximado de $\dpi{120} \pi$ é 3,14.

Área da lateral

A área da lateral de um cilindro é a área de um retângulo. Então, é só multiplicar o comprimento desse retângulo pela altura:

$\dpi{120} \acute{A}rea \ da \ lateral = 2 \pi r\cdot h$

Assim, temos a área total ou área externa de um cilindro:

$\dpi{120} \hspace{-0,5cm} \acute{A}rea\ total = {\color{Blue} \acute{A}rea \ das\ bases} + {\color{Magenta} \acute{A}rea\ da \ lateral} \\ \acute{A}rea \ total = 2\pi r^2 + 2 \pi rh\\ \acute{A}rea \ total = 2 \pi r(r +h)$ Volume de um cilindro

O volume de um cilindro é dado pela multiplicação entre a área da base (uma só) pela altura, isto é,

$\dpi{120} \hspace{-0,5cm} Volume \ do \ cilindro = \acute{a}rea \ da \ base \cdot h\\ Volume \ do \ cilindro = \pi r^2\cdot h$

Veja também: Circunferência – Definição, características e equação reduzida