Área do retângulo

Veja qual é a fórmula para calcular a área do retângulo e exemplos de como utilizá-la. Além disso, aprenda a calcular o perímetro e a encontrar a medida da diagonal.

Por Elainy Marciano Publicado em 07/02/2020 - 15:23

É necessário calcular a área de um retângulo quando, por exemplo, precisamos verificar quantos metros quadrados de cerâmica são necessários para fazer o piso do cômodo de uma casa ou saber o espaço ocupado por um canteiro retangular em um jardim.

Mas o que significa calcular a área de um retângulo? Significa calcular a medida da superfície ou medir o espaço ocupado por uma região retangular.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Então, vamos entender o que é um retângulo e depois aprender a calcular a área dessa importante figura geométrica.

O que é um retângulo?

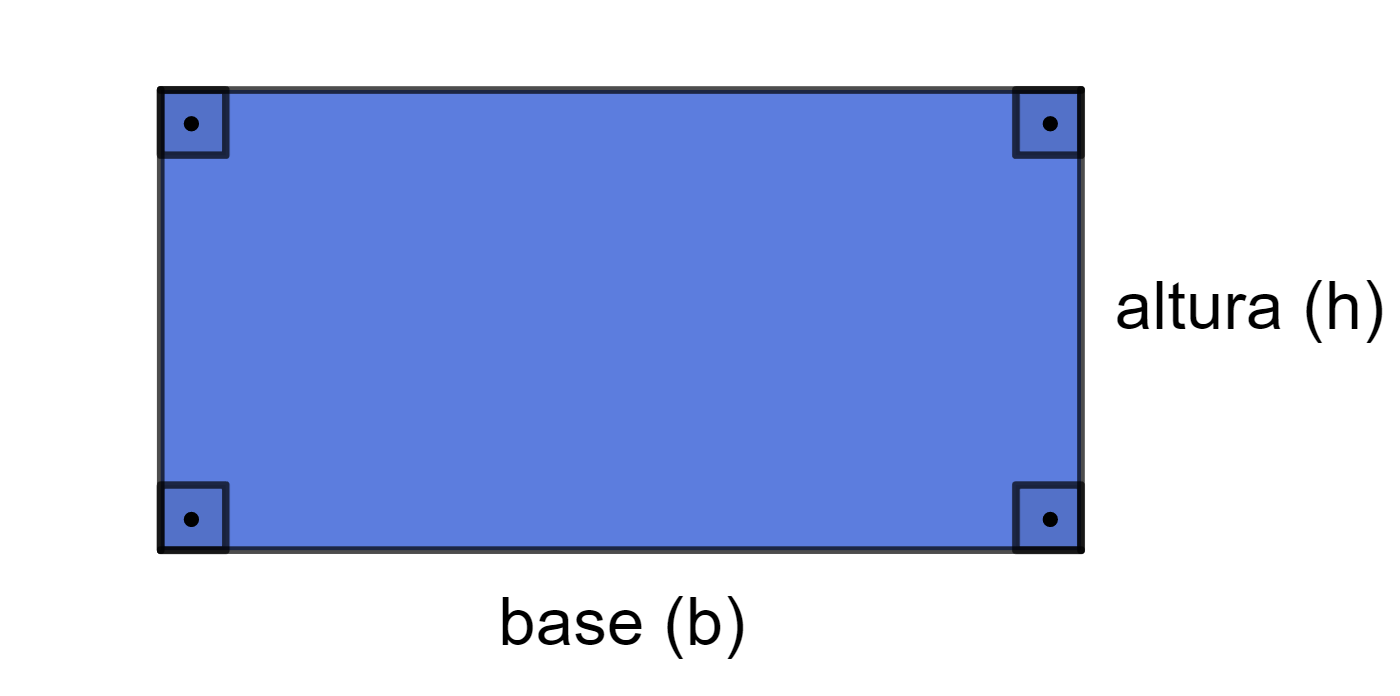
Um retângulo é um polígono de quatro lados, em que os lados opostos são paralelos e os quatro ângulos internos são ângulos retos, isto é, medem 90º.

O lado maior do retângulo é chamado de base e o lado menor é a altura.

Como calcular a área do retângulo?

Para calcular a área de qualquer retângulo, basta multiplicar a medida da base pela altura. Desse modo, a área do retângulo pode ser calculada pela seguinte fórmula:

$\dpi{120} \acute{A}rea \ do \ ret\hat{a}ngulo = b\cdot h$

em que:

$\dpi{120} b$ → é a medida da base do retângulo
$\dpi{120} h$ → é a altura do retângulo

Observação importante: Para calcular a área de um retângulo, é necessário que a medida da base e da altura estejam na mesma unidade de medida.

Se forem medidas diferentes, uma em metros e a outra em centímetros, por exemplo, devemos fazer a transformação para a mesma unidade de medida de comprimento antes de calcular a área.

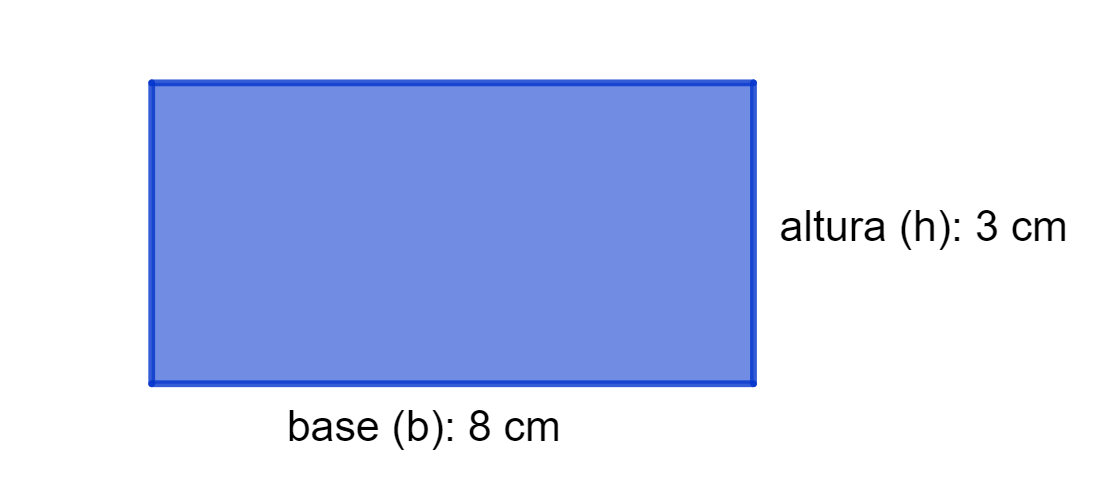
Exemplo 1: Calcular a área do retângulo abaixo:

A medida da base e a altura foram dadas, ambas, em centímetros. Então, não precisamos fazer nenhuma transformação. Usando a fórmula, temos que:

$\dpi{120} \flushleft \textit{A} = \textit{b \cdot\ h}\\ \textit{A} = 8 cm \cdot \ 3 \ \textnormal{cm}\\ \textit{A} = 24 cm^2$

Assim, esse retângulo tem 24 cm² de área.

Exemplo 2: Quantos metros quadrados de grama são necessários para cobrir um terreno retangular com base medindo 12 metros e altura igual a 6 metros?

A área do retângulo é a medida da sua superfície, assim, para saber a quantidade necessária de grama para cobrir esse terreno retangular, basta saber a sua área.

As duas medidas do terreno são dadas em metros, temos $\dpi{120} b = 12 \ \textnormal{m}$ e $\dpi{120} h = 6 \ \textnormal{m}$ . Então, vamos aplicar a fórmula:

$\dpi{120} \flushleft \textit{A} = \textit{b \cdot\ h}\\ \textit{A} = 12 m \cdot \ 6 \ \textnormal{m}\\ \textit{A} = 72 m^2$

Logo, são necessários 72 m² de grama para cobrir todo esse terreno.

Perímetro do retângulo

O perímetro de um retângulo é a medida do comprimento da sua borda. Desse modo, basta somar as medidas dos seus quatro lados para obtermos o perímetro.

Como os lados paralelos de um retângulo têm a mesma medida, temos dois lados com medida igual a $\dpi{120} b$ e dois lados com medida igual a $\dpi{120} h$ . Então, a soma dessas medidas é dada por: $\dpi{120} 2b +2h = 2\cdot (b+h)$ .

Assim, temos a fórmula para o cálculo do perímetro do retângulo:

$\dpi{120} Per\acute{\imath}metro \ do \ ret\hat{a}ngulo= 2\cdot (b+h)$

Exemplo 3: Vamos calcular o perímetro do retângulo do Exemplo 1:

$\dpi{120} \flushleft \textit{P} = 2 \cdot (8 \ \textnormal{cm} + 3 \ \textnormal{cm})\\ \textit{P} = 2 \cdot 11 \ \textnormal{cm} \\ \textit{P} = 22 \textnormal{cm}$

Então, o perímetro do retângulo do Exemplo 1 é igual a 22 cm.

Exemplo 4: Quantos metros uma pessoa vai andar se der uma volta completa no terreno retangular do Exemplo 2?

A medida de uma volta completa no terreno é a medida do perímetro dessa região retangular. Então, vamos calcular o perímetro:

$\dpi{120} \flushleft \textit{P} = 2 \cdot (12 \ \textnormal{m} + 6 \ \textnormal{m})\\ \textit{P} = 2 \cdot 18 \ \textnormal{m} \\ \textit{P} = 36 \textnormal{m}$

Assim, uma pessoa andará 36 m se der uma volta completa no terreno.

Diagonal do retângulo

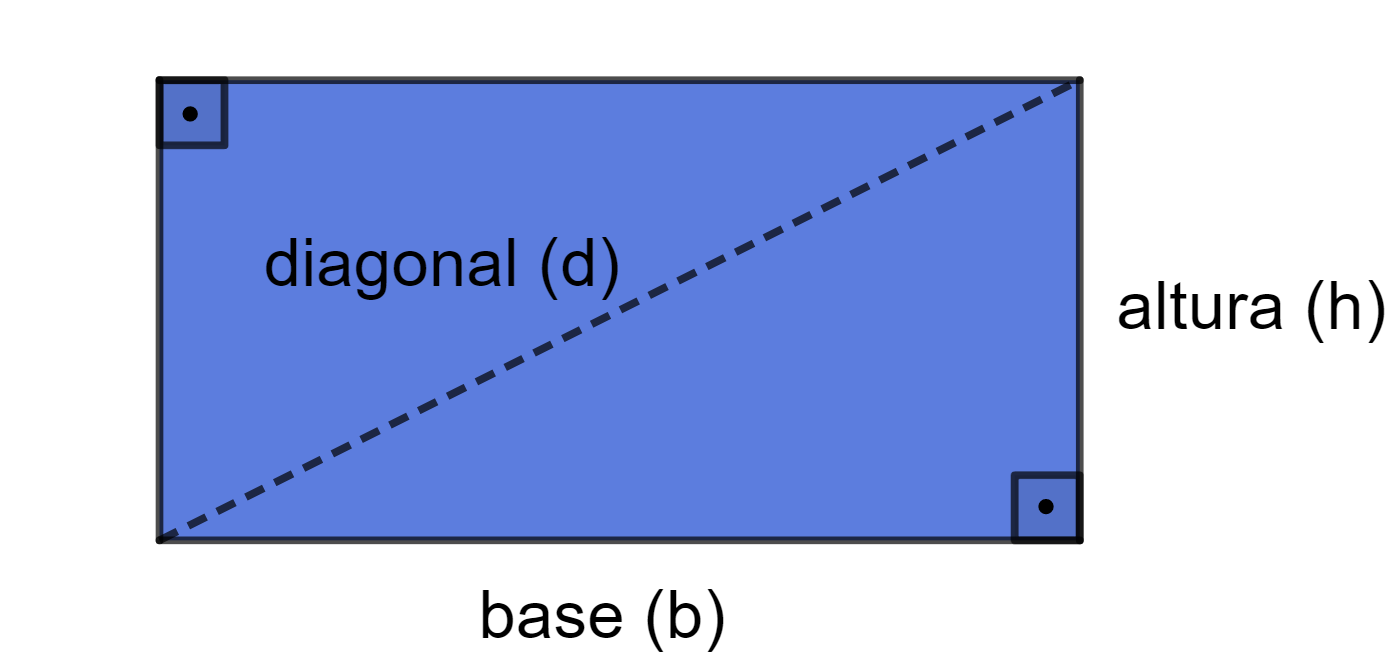
A diagonal do retângulo é um segmento de reta que o divide em dois triângulos retângulos (triângulos que possuem um ângulo de 90º).

Então, como você pode observar, a diagonal é um lado com valor desconhecido em um triângulo retângulo.

Assim, o que temos que fazer é descobrir a medida desse lado, mais especificamente, descobrir o valor da hipotenusa de um triângulo retângulo.

Para isso, vamos utilizar o Teorema de Pitágoras, que diz que a hipotenusa ao quadrado é igual a soma dos quadrados dos catetos.

Então, a diagonal (d) se relaciona com a medida da base (b) e da altura (h) de um retângulo, da seguinte forma: $\dpi{120} d^2 = b^2 + h^2$ Aplicando a raiz quadrada em ambos os lados da equação, temos que a fórmula para calcular a diagonal de um retângulo é:

$\dpi{120} d = \sqrt{b^2+h^2}$

Exemplo 5: Encontrar a medida da diagonal do retângulo do Exemplo 1:

$\dpi{120} \flushleft \textit{d} = \sqrt{b^2+h^2} \\ \textit{d} = \sqrt{(8 \ \textnormal{cm})^2+(3\ \textnormal{cm})^2} \\ \textit{d} = \sqrt{64 \ \textnormal{cm}^2+9 \ \textnormal{cm}^2}\\ \textit{d} = \sqrt{73\ \textnormal{cm}^2}\\ \textit{d} \approx 8,54 \ \textnormal{cm}$

Ou seja, a diagonal do retângulo do Exemplo 1 mede aproximadamente 8,54 cm.

Veja também: