Escalonamento de matrizes – Resolver sistemas lineares
Aprenda a resolver sistemas lineares que possuem um número diferente de equações e incógnitas pelo método do escalonamento. Veja exemplos de matrizes escalonadas.
O escalonamento de matrizes é um procedimento algébrico que podemos utilizar para resolver sistemas lineares onde o número de equações não é, necessariamente, igual ao número de incógnitas.
Resolver um sistema linear significa encontrar os valores das incógnitas que satisfazem todas as equações simultaneamente. No método do escalonamento, o objetivo é encontrar um sistema linear equivalente, mas que seja mais fácil de resolver do que o sistema inicial.
Para isso, utilizamos a matriz associada ao sistema linear e obtemos a forma escalonada dessa matriz. A partir da forma escalonada, a solução do sistema é obtida com facilidade.
Matriz escalonada
A forma de uma matriz escalonada depende da quantidade de linhas e colunas, ou seja, da quantidade de equações e da quantidade de incógnitas no sistema linear.
Considerando um sistema com mesmo número de equações e de incógnitas, a matriz escalonada será uma matriz triangular superior, que é uma matriz onde todos os elementos abaixo da diagonal principal são iguais a zero.
Exemplos de matrizes escalonadas:
Como fazer o escalonamento
Considerando um sistema linear, o primeiro passo é escrever a matriz associada a esse sistema, que é uma matriz formada por todos os coeficientes das equações e pelos termos independentes (aqueles após a igualdade).
Como vimos nos exemplos anteriores, matrizes escalonadas possuem alguns elementos iguais a zero. Então, o nosso objetivo ao escalonar uma matriz qualquer, é tornar alguns elementos iguais a zero.
Para isso, podemos fazer algumas operações entre as linhas da matriz:
- Trocar duas linhas de lugar;
- Somar ou subtrair uma linha por outra;
- Multiplicar ou dividir uma linha por um número real diferente de zero.
Exemplo: Vamos resolver o sistema linear abaixo para encontrar os valores de x, y e z.
Primeiro, vamos escrever a matriz de coeficientes e termos independentes e indicar cada uma das três linhas da matriz.
Escalonar essa matriz, significa zerar o primeiro elemento da segunda linha, e o primeiro e o segundo elemento da terceira linha.
1º objetivo: zerar o primeiro elemento da segunda linha.
Vamos multiplicar cada elemento da linha 2 pelo número 2 e subtrair cada valor da linha 1 multiplicado por 3.
2º objetivo: zerar o primeiro elemento da terceira linha.
Vamos multiplicar cada elemento da linha 3 pelo número 2 e subtrair cada elemento da linha 1 multiplicado por 5.
3º objetivo: zerar o segundo elemento da terceira linha.
Vamos subtrair da linha 3 cada elemento da linha 2 multiplicado pelo número 3.
A matriz está escalonada!
Agora, vamos reescrever o sistema linear, considerando a matriz escalonada.
Esse sistema escalonado é equivalente ao sistema inicial, porém muito mais fácil de determinar a solução.
Na equação 3 temos que:
-14z = 42 ⇒ z = -42/14 ⇒ z = -3
Substituindo o valor de z por -3 na equação 2, temos que:
y + 10z = -28 ⇒ y + 10.(-3) = -28 ⇒ y – 30 = -28
⇒ y = -28 + 30 ⇒ y = 2
Substituindo o valor de z por -3 e o valor de y por 2 na equação 1, temos que:
2x + y -2z = 10 ⇒ 2x + 2 – 2.(-3) = 10 ⇒ 2x + 2 + 6 = 10
⇒ 2x = 20 – 8 ⇒ 2x = 2 ⇒ x = 2/2 ⇒ x = 1
Portanto, a solução do sistema é S = {1, 2, -3}.
Observações:
- Se no escalonamento da matriz, todos os elementos de uma linha zerarem, então o sistema possui infinitas soluções.
- Se no escalonamento da matriz, todos os coeficientes de uma linha zerarem, mas o termo independente for diferente de zero, então o sistema não possui solução.
Você também pode se interessar:
- Tipos de matrizes
- Determinante de uma matriz
- Multiplicação de matrizes
- Adição e subtração de matrizes


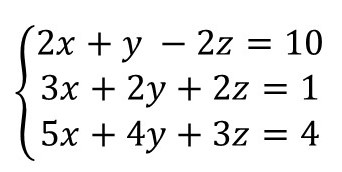
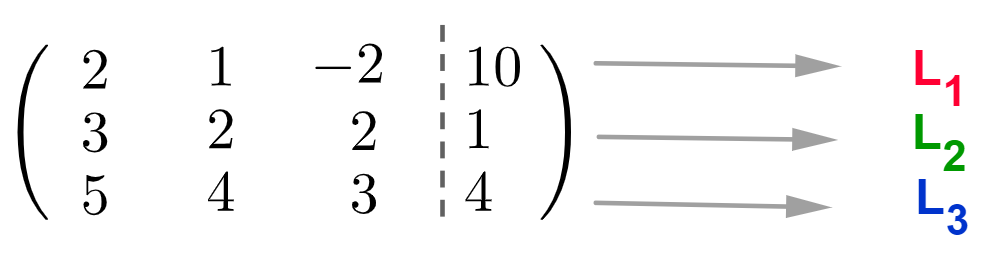

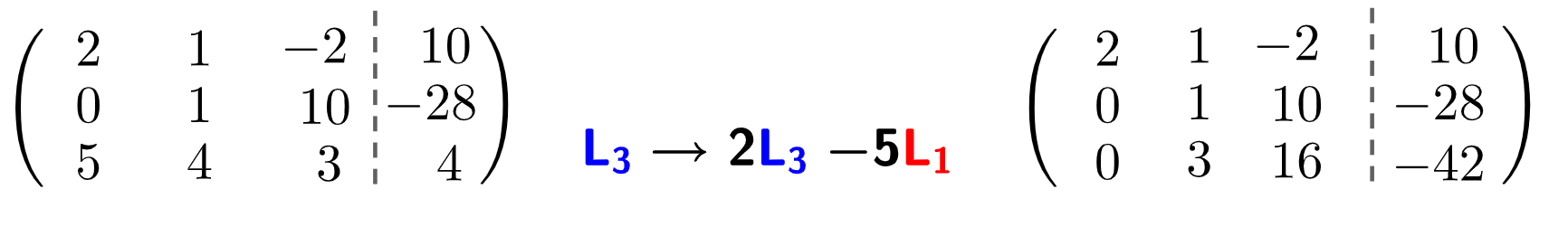

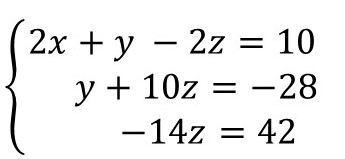
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.