Lista de exercícios sobre área dos setores circulares

Confira uma lista de exercícios resolvidos, passo a passo, sobre área dos setores circulares.

Por Elainy Marciano Publicado em 03/11/2020 - 18:20

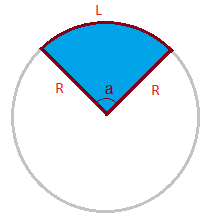
O setor circular é uma parte do círculo formada por dois raios e um arco, conforme apresentado na figura abaixo.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

R: raio do setor circular;
a: ângulo central;
L: comprimento do arco.

Para calcular a área do setor circular, podemos considerar três fórmulas:

→ A partir do ângulo central em graus:

$\dpi{120} \mathbf{A = \frac{a \cdot \boldsymbol{\pi} R^2}{360^{\circ}}}$

→ A partir do ângulo central em radianos:

$\dpi{120} \mathbf{A = \frac{a\cdot R^2}{2}}$

→ A partir do comprimento do arco:

$\dpi{120} \mathbf{A = \frac{L\cdot R}{2}}$

Além disso, temos que $\dpi{120} \mathbf{L = a\cdot R}$ .

Para praticar e aprender mais, confira uma lista de exercícios sobre área dos setores circulares, todos resolvidos passo a passo.

Exercícios sobre área dos setores circulares

Questão 1. Determine a área do setor circular de raio √5 cm e ângulo central igual a 30°.

Questão 2. Determine a área do setor circular de raio 2 m e ângulo central π/3 rad.

Questão 3. Determine a área de um setor circular, sabendo que o produto do arco e do raio é igual a 18π cm².

Questão 4. Determine a área do setor circular de ângulo central igual 3π/10 rad e comprimento de arco √3π cm.

Questão 5. Qual deve ser o comprimento do arco de um setor circular para sua área seja igual a 2R m²?

Resolução da questão 1

Temos R = √5 cm e a = 30°. Então, utilizaremos a seguinte fórmula da área:

$\dpi{120} \mathrm{A = \frac{a \cdot \pi R^2}{360^{\circ}}}$

Substituindo os valores na fórmula, temos que:

$\dpi{120} \mathrm{A = \frac{30^{\circ} \cdot \pi \cdot (\sqrt{5})^2}{360^{\circ}}}$

$\dpi{120} \Rightarrow \mathrm{A = \frac{1\cdot \pi\cdot 5}{12}}$

$\dpi{120} \Rightarrow \mathrm{A = \frac{5}{12}\cdot \pi}$

Portanto, a área é igual a 5/12 π cm².

Resolução da questão 2

Temos R = 2 m e a = π/3 rad. Então, utilizaremos a seguinte fórmula:

$\dpi{120} \mathrm{A = \frac{a\cdot R^2}{2}}$

Substituindo os valores na fórmula, temos que:

$\dpi{120} \mathrm{A = \frac{\frac{\pi}{3}\cdot 2^2}{2}}$

$\dpi{120} \Rightarrow \mathrm{A = \frac{2}{3}\pi}$

Portanto, a área é igual a 2/3π m².

Resolução da questão 3

Temos L . R = 18π cm². Então, vamos utilizar a seguinte fórmula:

$\dpi{120} \mathrm{A = \frac{L\cdot R}{2}}$

Substituindo os valores na fórmula, temos que:

$\dpi{120} \mathrm{A = \frac{18 \pi}{2}}$

$\dpi{120} \Rightarrow \mathrm{A = 9 \pi}$

Portanto, a área é igual a 9π cm².

Resolução da questão 4

Temos a = 3π/10 rad e L = √3π cm. Precisamos de uma fórmula da área em função dessas duas medidas.

Como $\dpi{120} \mathrm{L = a\cdot R}$ , então:

$\dpi{120} \Rightarrow \mathrm{R = \frac{L}{a}}$

Assim:

$\dpi{120} \mathrm{A = \frac{L\cdot R}{2} = \frac{L.\frac{L}{a}}{2} = \frac{L^2}{2a}}$

Substituindo os valores na fórmula, temos que:

$\dpi{120} \mathrm{A = \frac{(\sqrt{3}\pi)^2}{2\cdot \frac{3\pi}{10}}}$

$\dpi{120} \Rightarrow \mathrm{A = \frac{3\pi^2}{ \frac{3\pi}{5}}}$

$\dpi{120} \Rightarrow \mathrm{A = \frac{15\pi^2}{ 3 \pi}}$

$\dpi{120} \Rightarrow \mathrm{A = 5 \pi}$

Portanto, a área é igual a 5π cm².

Resolução da questão 5

Temos A = 2R m². Considerando a seguinte fórmula:

$\dpi{120} \mathrm{A = \frac{L\cdot R}{2}}$

Temos que: $\dpi{120} \mathrm{2R = \frac{L\cdot R}{2}}$

$\dpi{120} \Rightarrow \mathrm{4\cancel{R} = L.\cancel{R}}$

$\dpi{120} \mathrm{\Rightarrow L = 4}$

Portanto, o comprimento do arco deve ser igual a 4 m.

Para baixar essa lista de exercícios sobre área do setor circular em PDF, clique aqui!

Você também pode se interessar:

Geometria plana

Elainy Marciano

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.