Lista de exercícios sobre comprimento da circunferência

Quer aprender a resolver problemas envolvendo comprimento da circunferência? Confira uma lista de exercícios resolvidos que preparamos sobre esse assunto!

Por Elainy Marciano Publicado em 23/06/2020 - 16:46

Muitos problemas envolvendo coisas ou objetos de forma circular se resumem ao cálculo do comprimento da circunferência.

O comprimento C de uma circunferência pode ser calculado pela seguinte fórmula:

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

$\dpi{120} \mathrm{C = 2\cdot \pi \cdot r}$

Sendo r a medida do raio da circunferência.

Para saber mais sobre esse assunto, confira uma lista de exercícios sobre comprimento da circunferência, todos resolvidos e com gabarito.

Lista de exercícios sobre comprimento da circunferência

Questão 1. Deseja-se pregar uma fita decorativa ao redor da tampa de um pote redondo. Se o diâmetro da tampa mede 12 cm, qual o comprimento mínimo que a fita deve ter para dar a volta completa na tampa?

Questão 2. O contorno de uma peça circular tem 190 cm de comprimento. Qual a medida do diâmetro dessa peça?

Questão 3. A roda de um ônibus tem 90 cm de raio. Que distância o ônibus terá percorrido quando a roda der 120 voltas?

Questão 4. Qual é a área de um círculo cuja circunferência tem 40 metros de comprimento?

Questão 5. Um círculo tem 18 cm² de área. Qual é o seu perímetro?

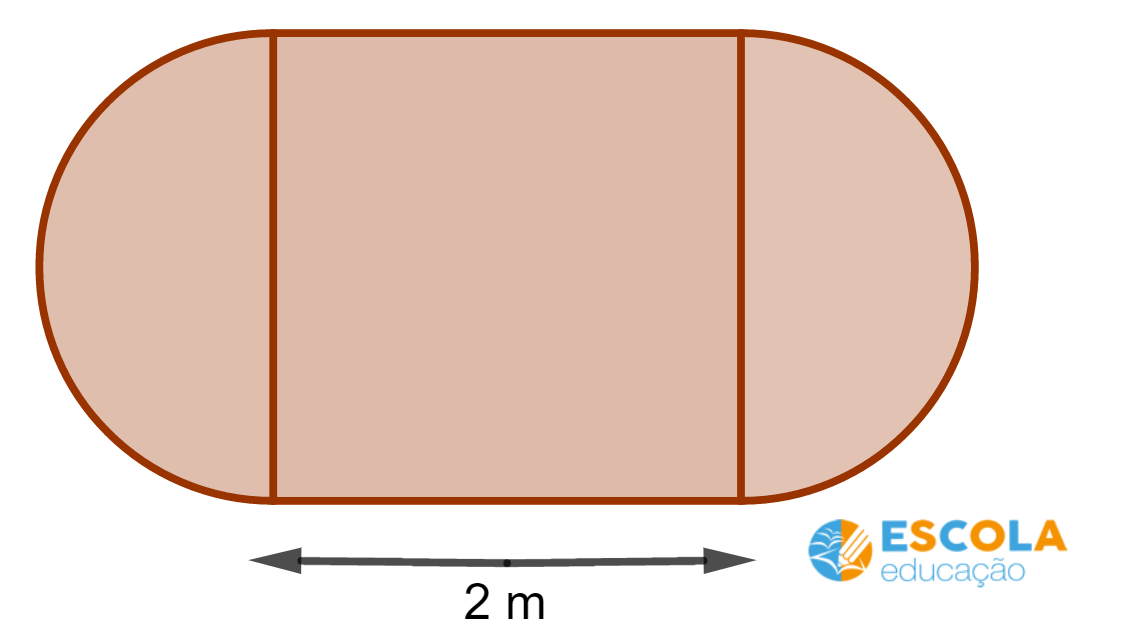
Questão 6. A superfície de uma mesa é formada por um quadrado de lado igual a 2 m e dois semicírculos, um em cada lateral, conforme mostra a figura.

Calcule o perímetro e a área da superfície da mesa.

Resolução da questão 1

A medida do contorno do pote corresponde ao comprimento de uma circunferência com diâmetro igual a 12 cm.

Para calcular o comprimento, precisamos do raio.

O raio de uma circunferência é igual à metade da medida do diâmetro, então, o raio é igual a 6 cm.

Substituindo r por 6 e $\dpi{120} \pi$ por 3,14, na fórmula do comprimento da circunferência, temos que:

$\dpi{120} \mathrm{C = 2\cdot 3,14 \cdot 12}$

$\dpi{120} \Rightarrow \mathrm{C = 75,36}$

Como a medida do raio está em centímetros, o resultado do comprimento também será em centímetros.

Logo, a fita deve ter no mínimo 75,36 centímetros de comprimento para dar a volta completa na tampa do pote.

Resolução da questão 2

Sabendo a medida do comprimento de uma circunferência, podemos determinar o valor do raio.

Veja que substituindo C por 190 e $\dpi{120} \pi$ por 3,14 na fórmula, temos que:

$\dpi{120} \mathrm{190 = 2\cdot 3,14 \cdot r}$

$\dpi{120} \Rightarrow \mathrm{190 = 6,28\cdot r}$

$\dpi{120} \Rightarrow \mathrm{r = 30,24}$

Com a medida do raio, podemos determinar o diâmetro.

$\dpi{120} \mathrm{D = 2\cdot r}$

$\dpi{120} \Rightarrow \mathrm{D = 2\cdot 30,24}$

$\dpi{120} \Rightarrow \mathrm{D = 60,48}$

Como a medida do comprimento foi dada em centímetros, então, o raio e o diâmetro calculados também estão em centímetros.

Assim, o diâmetro da peça mede 60,48 cm.

Resolução da questão 3

Em cada volta que a roda dá, a distância percorrida é igual à medida do comprimento do contorno da roda.

Assim, o que temos que fazer é calcular tal comprimento e depois multiplicar o valor obtido por 120, que é o número total de voltas.

Substituindo r por 90 e $\dpi{120} \pi$ por 3,14 na fórmula do comprimento, obtemos:

$\dpi{120} \mathrm{C = 2\cdot 3,14 \cdot 90}$

$\dpi{120} \Rightarrow \mathrm{C = 565,2}$

Então, o comprimento do contorno da roda é igual a 565,2 cm.

Vamos multiplicar por 120 para obter a distância percorrida:

565,2 × 120 = 67824

Até agora, utilizamos as medidas em centímetros, então, o resultado também está em centímetros.

Para indicar a distância percorrida pelo ônibus, vamos fazer a transformação para metros:

67824 : 100 = 678,24

Portanto, a distância percorrida pelo ônibus foi de 678,24 metros.

Resolução da questão 4

A área do círculo depende da medida do raio.

Para saber a medida do raio, vamos utilizar a informação do comprimento da circunferência:

$\dpi{120} \mathrm{40 = 2\cdot 3,14 \cdot r}$

$\dpi{120} \Rightarrow \mathrm{40 = 6,28 \cdot r}$

$\dpi{120} \Rightarrow \mathrm{r = 6,37}$

Agora, já podemos calcular a área do círculo:

$\dpi{120} \mathrm{A = \pi\cdot r^2}$

$\dpi{120} \Rightarrow \mathrm{A =3,14\cdot (6,37)^2}$

$\dpi{120} \Rightarrow \mathrm{A =127,4}$

As medidas utilizadas estavam em metros, então, a área será em metros ao quadrado. Portanto, a área do círculo é igual a 127,4 m².

Resolução da questão 5

O perímetro de um círculo corresponde a medida do seu contorno, que é o comprimento da circunferência.

O comprimento da circunferência depende do valor do raio. Para determinar esse valor, vamos utilizar a informação da área do círculo:

$\dpi{120} \mathrm{A = \pi\cdot r^2}$

$\dpi{120} \Rightarrow \mathrm{18 =3,14\cdot r^2}$

$\dpi{120} \Rightarrow \mathrm{r^2 = \frac{18}{3,14}}$

$\dpi{120} \Rightarrow \mathrm{r^2 = 5,7325}$

$\dpi{120} \Rightarrow \mathrm{r = 2,393}$

Agora que já sabemos a medida do raio, podemos calcular o comprimento da circunferência:

$\dpi{120} \mathrm{C = 2\cdot 3,14 \cdot 2,393}$

$\dpi{120} \Rightarrow \mathrm{C = 15,01}$

Portanto, o comprimento da circunferência (perímetro do círculo) é igual a 15,01 cm.

Resolução da questão 6

O perímetro corresponde a medida do contorno da figura. Assim, basta calcular o perímetro do círculo e somar com os dois lados do quadrado.

Perímetro do círculo:

O círculo tem diâmetro igual a 2 (é o lado do quadrado), logo, o raio é igual a 1.

Pela fórmula do comprimento da circunferência, temos que:

$\dpi{120} \mathrm{C = 2\cdot 3,14 \cdot 1}$

$\dpi{120} \mathrm{C = 6,28}$

O que significa que o círculo tem 6,28 metros de perímetro.

Perímetro da superfície da mesa:

P = 6,28 + 2 + 2

P = 10,28

Logo, o perímetro da superfície da mesa mede 10,28 metros.

Para o cálculo da área da superfície, o procedimento é semelhante. Calculamos a área do círculo e somamos com a área do quadrado.

A área do quadrado de lado 2 m é igual a 4 m².

Área do círculo de raio 1:

$\dpi{120} \mathrm{A = 3,14\cdot 1^2 = 3,14}$

Área da superfície da mesa:

A = 4 + 3,14 = 7,14

Portanto, a área da superfície da mesa é igual a 7,14 m².

Você também pode se interessar: