Função exponencial
Conheça a função exponencial e suas características, saiba como é o seu gráfico e quando a curva é crescente ou decrescente.
A função exponencial é qualquer função do tipo:
Em que e
e
é a variável.
Para ser uma função exponencial, a variável deve ser sempre o expoente e não contrário.
Exemplos de função exponencial:
Exemplos de funções que não são exponenciais: ,
,
.
Domínio e imagem da função exponencial
O domínio da função exponencial corresponde ao conjunto dos números reais, ou seja, não há restrições para o valor do expoente .
Já a imagem da função exponencial é igual ao conjunto dos números reais positivos, ou seja, os valores de são apenas valores maiores que 0.
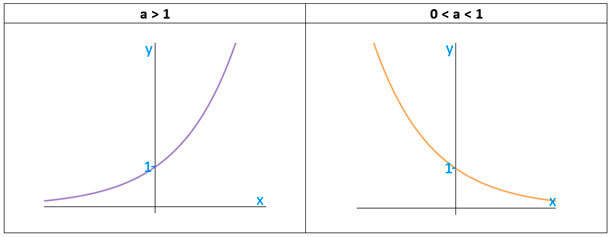
Gráfico da função exponencial
O gráfico da função exponencial é uma curva que sempre está sempre na parte onde Y é positivo, já que a imagem da função é sempre um valor positivo.
Além disso, como qualquer valor elevado a 0 é sempre 1, então, na função exponencial temos f(0) = 1 sempre. Dessa forma, a curva da função exponencial sempre passa pelo ponto (0,1).
A curva da função é crescente ou decrescente de acordo com o valor da constante .
- Função exponencial crescente:
, com
.
- Função exponencial decrescente:
, com
.
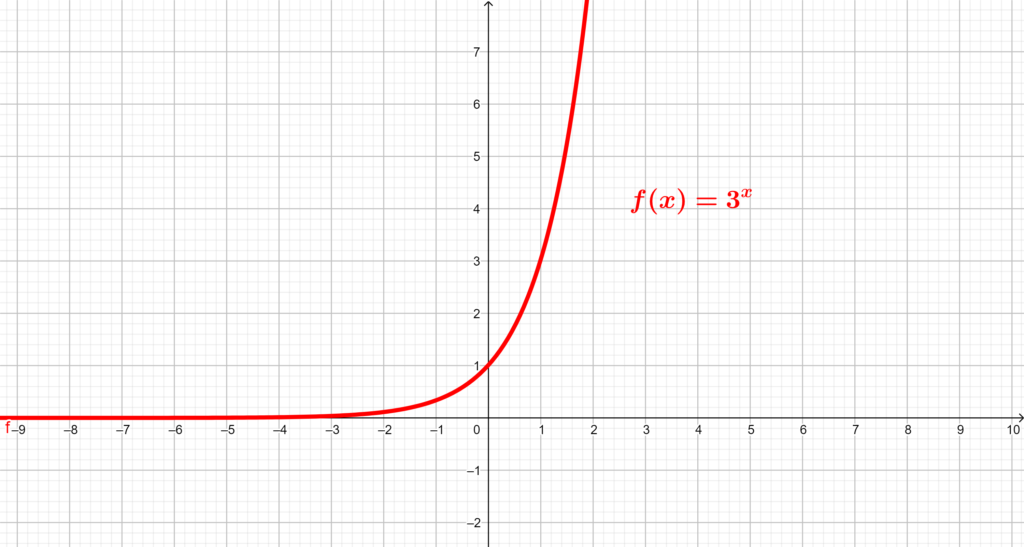
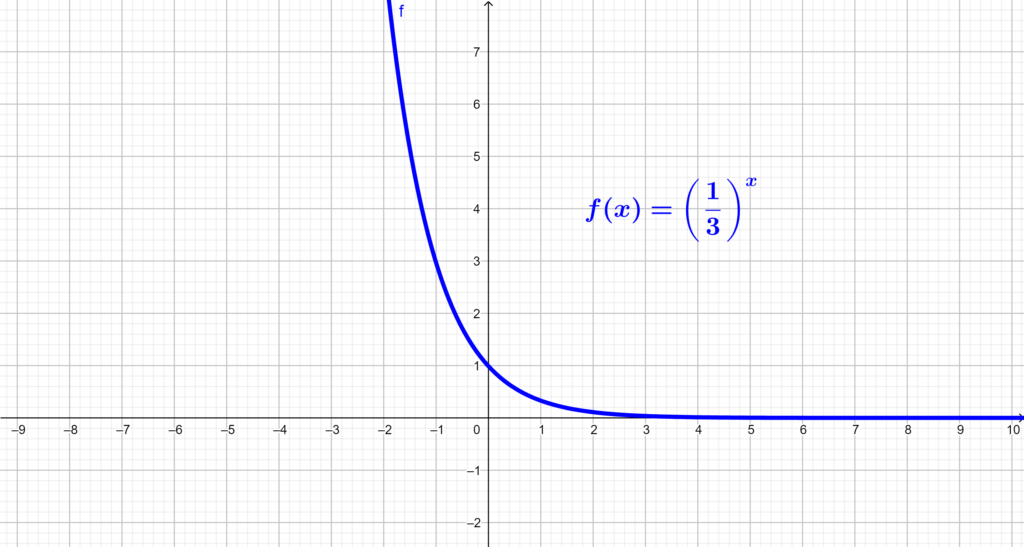
Exemplos: gráfico das funções exponenciais: e
.
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.