Função polinomial
Saiba tudo o que você precisa sobre a função polinomial. Aprenda a construir o gráfico, realizar operações e muito mais!
Uma função polinomial é qualquer função definida por um polinômio. A forma geral de uma função polinomial é:
Em que são coeficientes e
são as variáveis da função polinomial.
Grau dos polinômios
O grau de uma função polinomial corresponde ao grau do polinômio. Assim, se uma função é representada por um polinômio de grau n, a função polinomial também será de grau n.
Para determinar o grau dos polinômios, basta observar os expoentes das variáveis. O grau do polinômio é o valor do maior expoente.
Exemplos:
f(x) = x + 1 → polinômio de grau 1 → função polinomial de grau 1
f(x) = x² + 2x – 3 → polinômio de grau 2 → função polinomial de grau 2
f(x) = -x³ + 4x² – x + 2 → polinômio de grau 3 → função polinomial de grau 3
Valor numérico de um polinômio
O valor numérico de um polinômio é obtido quando substituímos as variáveis por um número.
Exemplo:
Para transportar uma carga, um caminhoneiro cobra o preço fixo de R$ 50,00 mais R$ 3,00 a cada quilômetro rodado.
Assim, se x é o número de quilômetros rodados, o preço do frete (P) pode ser representado por um polinômio: P = 3x + 50.
Supondo que foram rodados 100 km, ou seja, x = 100, o preço é dado por:
P = 3. 100 + 50 = 350
Portanto, quando x = 100, o valor numérico do polinômio é 350.
Gráficos da função polinomial
O gráfico da função polinomial dependerá do grau do polinômio. Em qualquer caso, o gráfico pode ser obtido da seguinte forma:
- Atribuímos valores para x e determinamos vários pares ordenados (x,y) que pertencem à função;
- Marcamos esses pares ordenados no plano cartesiano;
- Ligamos os pontos marcados para obter o esboço do gráfico.
A seguir, vamos ver os gráficos mais comuns, que são os gráficos das funções de grau 1, 2 e 3.
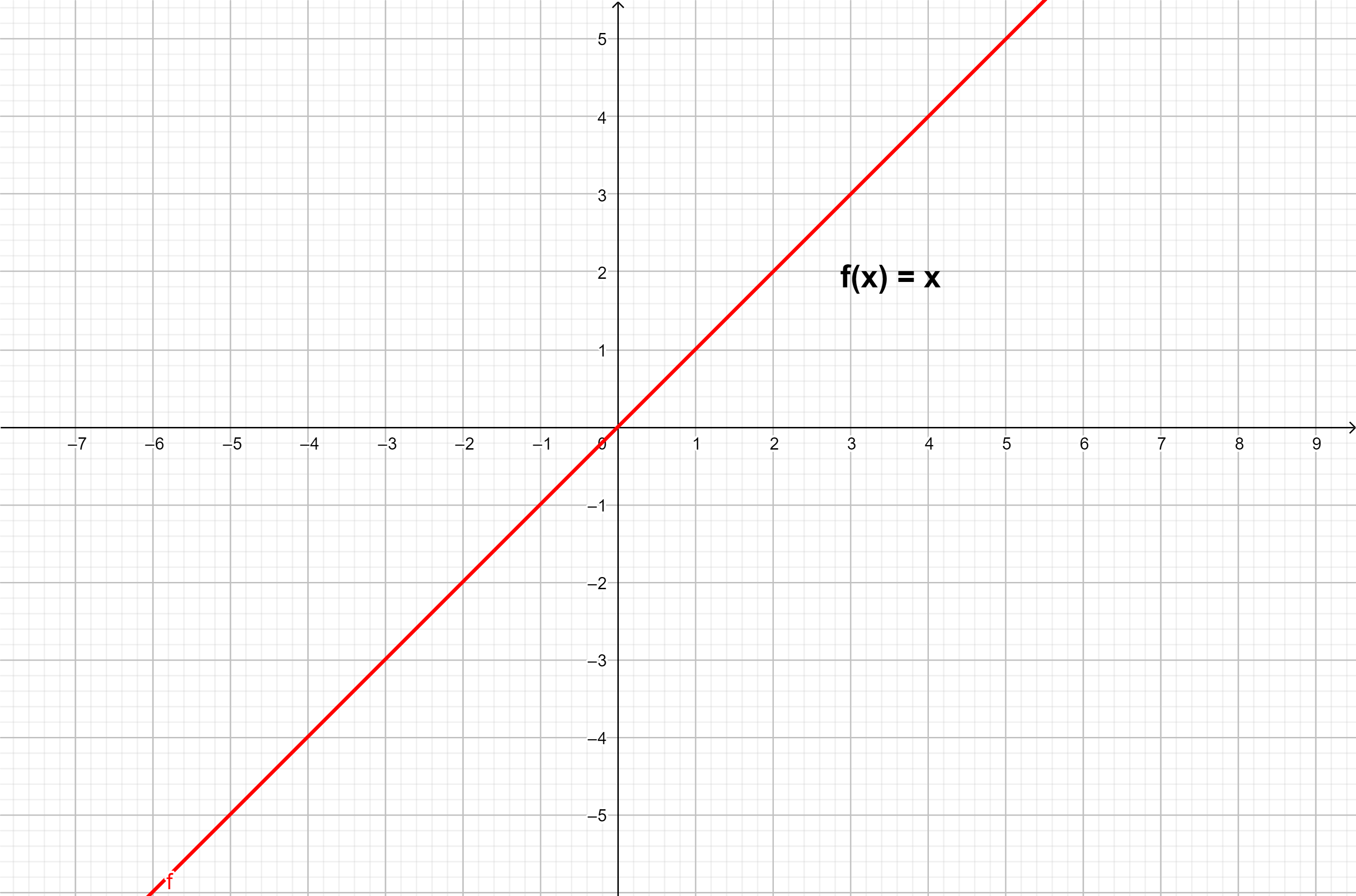
Função polinomial de grau 1
Uma função polinomial de grau 1 também é conhecida como função afim e o seu gráfico é sempre uma reta.
Exemplo: f(x) = x
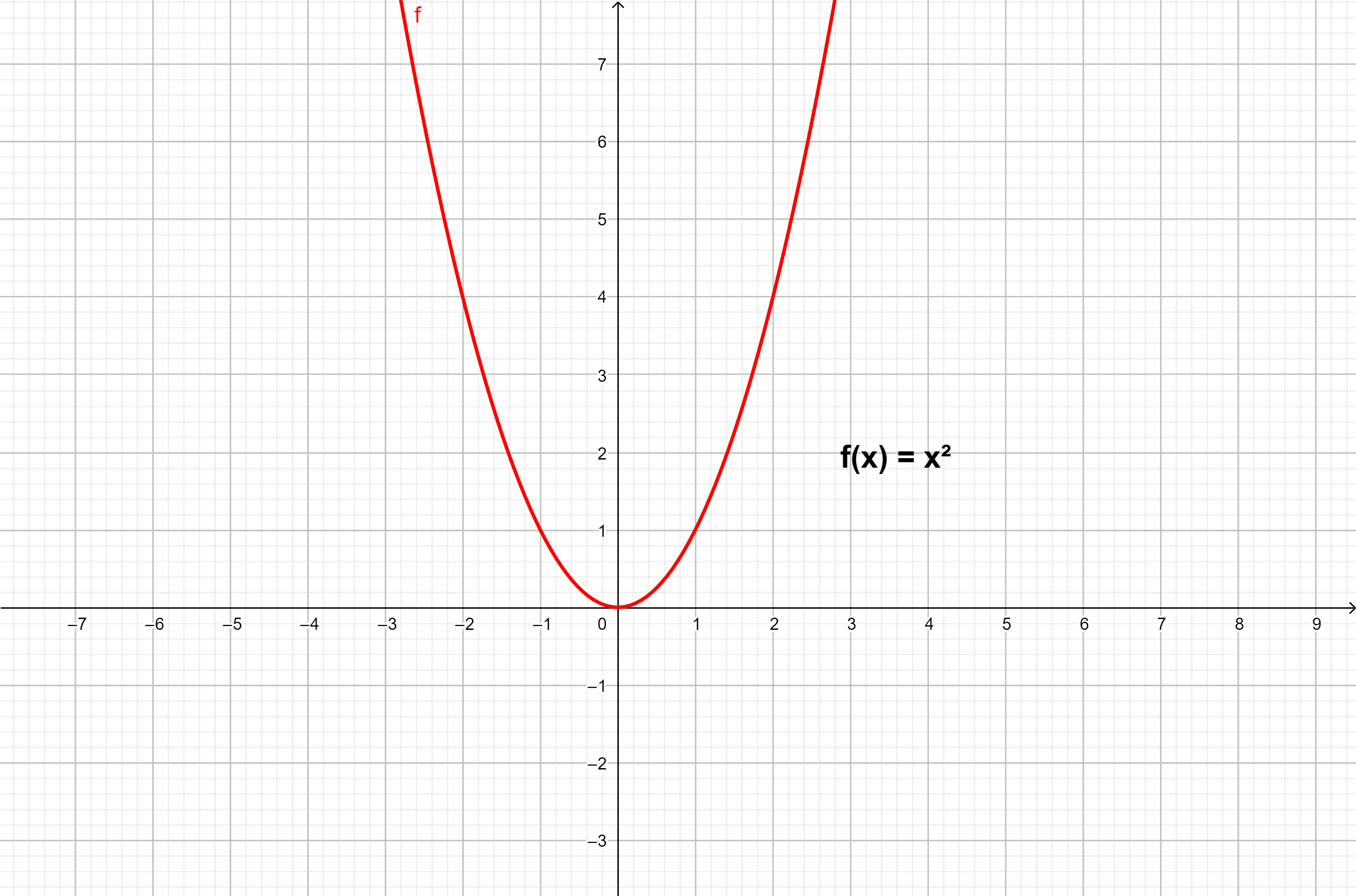
Função polinomial de grau 2
A função polinomial de grau 2 também é chamada de função quadrática e o seu gráfico é sempre uma parábola.
Exemplo: f(x) = x²
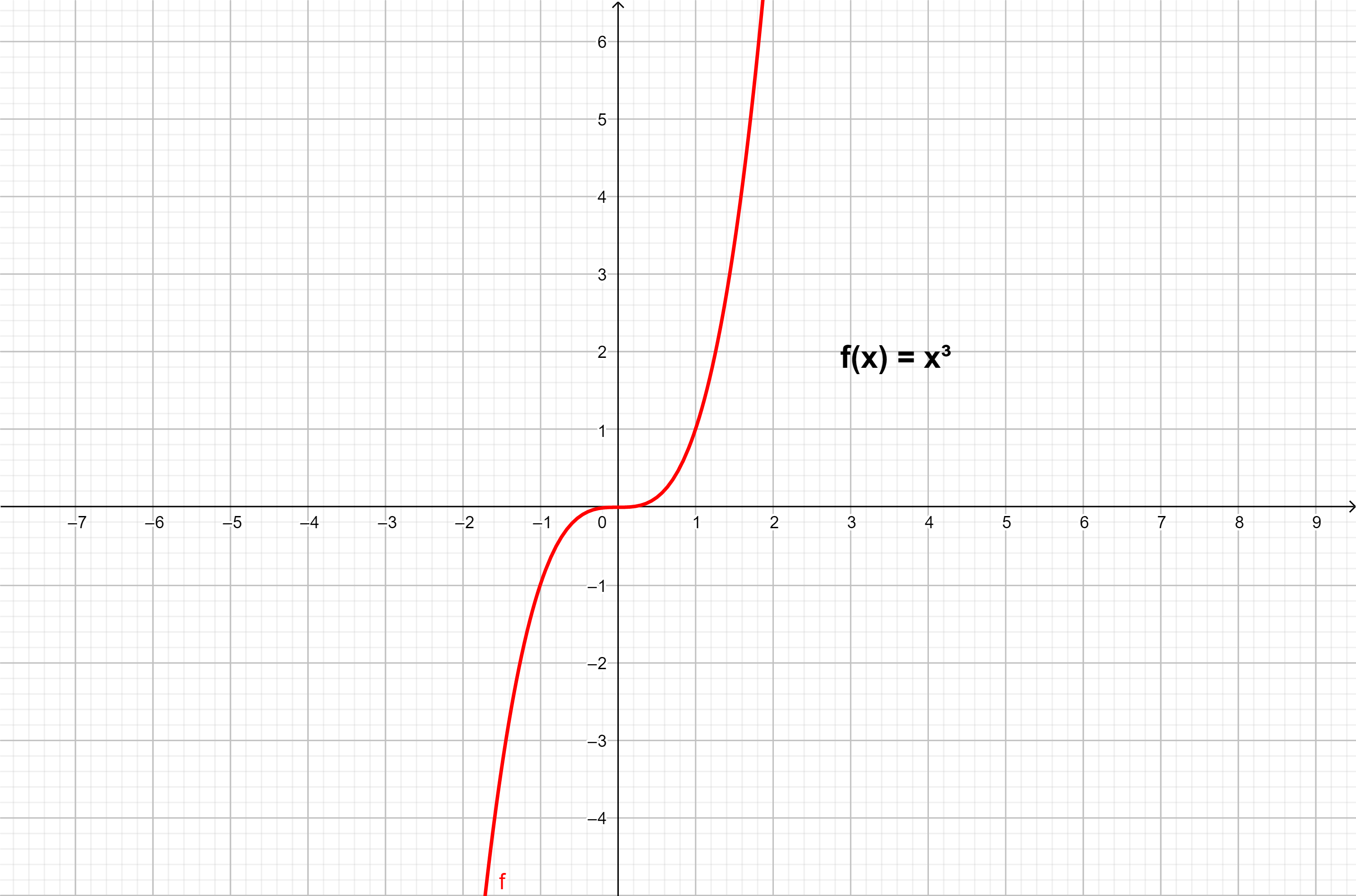
Função polinomial de grau 3
Veja o exemplo do gráfico de uma função polinomial de grau 3.
Exemplo: f(x) = x³
Igualdade de polinômios
A igualdade de dois polinômios ocorre quando os coeficientes correspondentes aos termos de mesmo grau são iguais.
Exemplo: considere f(x) = 2x³ – x + 4 e g(x) = ax³ + bx + c.
Esses dois polinômios serão iguais quando a = 2, b= -1 e c = 4.
Operações com polinômios
Adição de polinômios
A adição de polinômios é obtida quando somamos os coeficientes dos termos semelhantes.
Exemplo: (2x² – 3x – 5) + (x² + x – 2)
(2x² – 3x – 5) + (x² + x – 2) = 2x² – 3x – 5 + x² + x – 2 = 3x² – 2x – 7
Subtração de polinômios
A subtração de polinômios é obtida quando subtraímos os coeficientes dos termos semelhantes.
Exemplo: (2x² – 3x – 5) – (x² + x – 2)
(2x² – 3x – 5) – (x² + x – 2) = 2x² – 3x – 5 – x² – x + 2 = x² – 4x – 3
Multiplicação de polinômios
Na multiplicação de polinômios, multiplicamos cada termo do primeiro polinômio por cada um dos termos do segundo polinômio.
Exemplo: (x² – x + 2) . (x + 1)
(x² – x + 2) . (x + 1) = x³ + x² – x² – x + 2x + 2 = x³ + x + 2
Divisão de polinômios
Na divisão de polinômios, utilizamos o método da chave. Para compreender, veja um exemplo:
Exemplo: (x³ – 3x² – x + 6) : (x-2)
Teorema do resto
O teorema do resto diz que a divisão de um polinômio f(x) por x – a é igual ao valor da função f no ponto a, isto é, o resto R é dado por:
R = f(a)
Exemplo: o resto da divisão de f(x) = x³ – 2x + 7 por x – 1 é igual a 6, pois f(1) = 1³ – 2.1 + 7 = 6.
Você também pode se interessar:
- Exercícios sobre função quadrática
- Domínio, contradomínio e imagem
- Exercícios sobre coeficientes e concavidade da parábola


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.