Função linear

Uma função linear é uma função  do tipo:

em que  é um número real diferente de zero.

Algumas características da função linear:

• É um caso particular da função afim, , quando .
• O gráfico é sempre uma reta que passa pela origem (0,0);
• O número  é chamado de coeficiente angular e indica a inclinação da reta com relação ao eixo das abscissas.

Para cada valor de  diferente, temos uma função linear diferente. Quando , temos a função , que também é chamada de função identidade.

Veja outros exemplos de função linear quando variamos o valor do coeficiente angular :

• , temos 
• , temos 
• , temos 
• , temos 
• , temos 

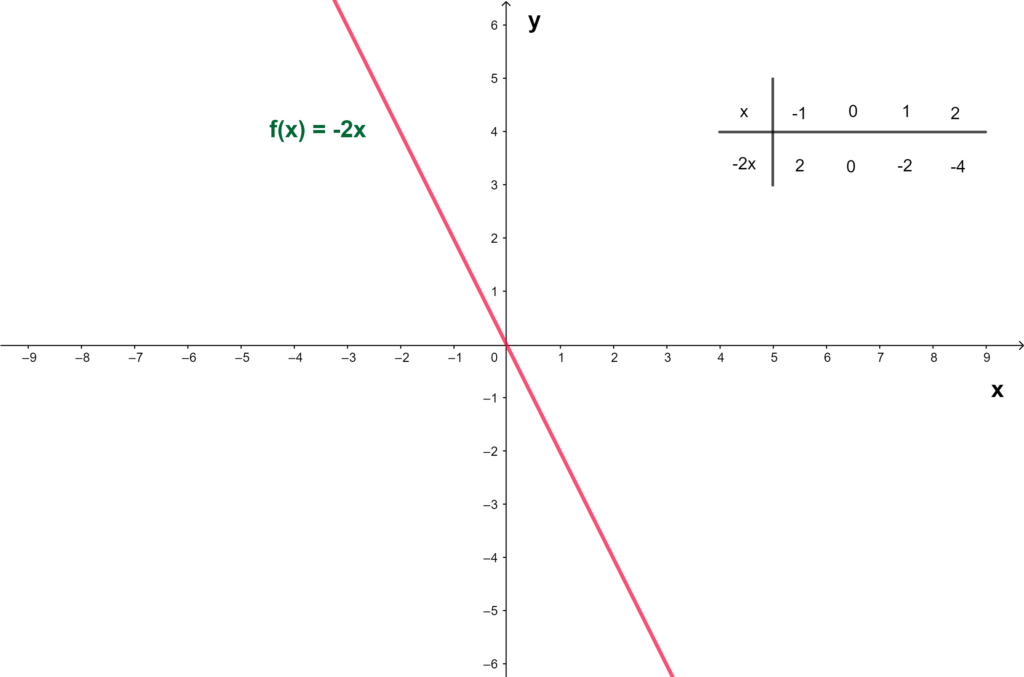
Gráfico da função linear

O gráfico da função linear é sempre uma reta que passa pelo ponto (0,0). Para traçar o gráfico da função, basta atribuir alguns valores de  e encontrar .

Exemplo:

Função crescente e decrescente

A função linear será crescente se o coeficiente angular for um valor maior que zero e será decrescente se ele for um valor menor que zero.

• Crescente: 
• Decrescente: 

Assim, uma função  é um exemplo de função linear crescente. Já uma função  é uma função linear decrescente.

Você também pode se interessar:

• Função polinomial
• Função quadrática
• Função injetora
• Domínio, contradomínio e imagem
• Funções trigonométricas – Seno, cosseno e tangente