Lista de exercícios de números decimais
Quando se trata de números decimais, muita gente costuma ter alguma dificuldade. Por isso, preparamos uma lista com 10 exercícios resolvidos sobre esse tema.
Os números decimais são utilizados para representar quantidades não inteiras e muitos problemas envolvem esse tipo de número.
A seguir, temos uma lista com 10 exercícios resolvidos sobre os números decimais.
Lista de exercícios de números decimais
Exercício 1
Escreva cada uma das frações como um número decimal:
Exercício 2
Escreva cada um dos números decimais em forma de fração:
Exercício 3
Qual é a fração escrita na forma simplificada, que corresponde ao número decimal 0,8?
Exercício 4
Resolva as seguintes somas de números decimais:
a) b)
Exercício 5
Resolva as seguintes subtrações de números decimais:
Exercício 6
Qual o valor da expressão 15 – 9,85 + 3,275?
Exercício 7
A altura de uma casa era 5,18 metros. Construído um segundo andar, a altura da casa passou a ser de 7,7 metros. Em quantos metros a altura inicial da casa foi aumentada?
Exercício 8
Resolva as seguintes operações com números decimais:
Exercício 9
Qual o resultado da multiplicação entre 0,96 e 0,5?
Exercício 10
Em uma competição automobilística, a distância é medida em milhas. Cada milha vale 1,6 quilômetro, aproximadamente. Quantas milhas há em 512 quilômetros?
Resolução do exercício 1
Para escrever um número fracionário na forma decimal, só temos que escrever o número do numerador e colocar uma vírgula nele deixando:
- Uma casa após a vírgula, se o denominador da fração é 10;
- Duas casas após a vírgula, se o denominador da fração é 100;
- Três casas após a vírgula, se o denominador da fração é 1000;
E assim por diante.
a) → Um número após a vírgula, pois o denominador é 10.
b) → Dois números após a vírgula, pois o denominador é 100.
Observe que só temos o número 52 e deixando duas casas após a vírgula, não sobra nenhum número na frente dela. Quando isso acontece, colocamos um 0 na frente da vírgula. Por isso ficou 0,52.
c) → Três números após a vírgula, pois o denominador é 1000.
Aqui, deveríamos deixar três números após a vírgula. Por isso, completamos o espaço vazio com 0 e temos 0,052.
Resolução do exercício 2
Para escrever um número decimal na forma fracionária, escrevemos o número sem a vírgula no numerador e, no denominador, escrevemos:
- 10, se o número tiver uma casa após a vírgula;
- 100, se o número tiver duas casas após a vírgula;
- 1000, se o número tiver três casas após a vírgula;
E assim por diante.
a) → Denominador 10, pois temos uma casa após a vírgula.
b) → Denominador 100, pois temos duas casas após a vírgula.
c) → Denominador 1000, pois temos três casas após a vírgula.
Resolução do exercício 3
Primeiro, escrevemos o número na forma de fração, assim como no exercício anterior.
Depois, simplificamos a fração:
Então, a fração simplificada que corresponde ao número 0,8 é a fração .
Resolução do exercício 4
a)
Para fazer essa soma, basta escrever décimos embaixo de décimos, vírgula embaixo de vírgula e unidade embaixo de unidade.
Depois, somamos normalmente, descendo a vírgula na mesma posição.
b)
Nessa conta, acrescentamos um 0 no final do número 0,85 para que ele tenha três casas após a vírgula assim como o número 1,376.
Resolução do exercício 5
a)
Para fazer essa subtração, basta escrever décimos embaixo de décimos, vírgula embaixo de vírgula, unidade embaixo de unidade e dezena embaixo de dezena.
Depois, subtraímos normalmente, descendo a vírgula na mesma posição.
b)
Nessa conta, acrescentamos uma vírgula e 00 no número 25 para que ele tenha duas casas após a vírgula assim como o número 18,25.
Resolução do exercício 6
Primeiro resolvemos a subtração 15 – 9,85:
Ao resultado obtido, somamos 3,275:
Resolução do exercício 7
Para resolver esse problema temos que subtrair a altura inicial da altura final, ou seja, resolver:
Assim, a altura da casa foi aumentada em 2,52 metros.
Resolução do exercício 8
Nesse exercício, vamos usar as regrinhas de deslocamento da vírgula na multiplicação e na divisão por 10, por 100 e por 1000.
Devemos lembrar que todos os números inteiros têm uma vírgula omitida, por exemplo o número 2 pode ser escrito como 2,0 ou 2,00, e assim por diante.
a) b)
c)
d) e)
f )
Resolução do exercício 9
Para fazer a multiplicação entre números decimais, basta fazer a conta dos números sem a vírgula: 096 x 05 = 0480.
Em seguida, somamos o número de casas após a vírgula nos fatores da multiplicação: três casas.
Então acrescentamos uma vírgula no resultado da multiplicação, deixando esse mesmo número de casas após a vírgula: 0,480.
Resolução do exercício 10
Para saber o total de milhas temos que dividir 512 por 1,6. Assim, temos uma divisão de um número inteiro por um número decimal:
Multiplicando o número 1,6 por 10 conseguimos omitir a vírgula:
Como multiplicamos o número 1,6 por 10, também devemos multiplicar o número 512 por 10:
Assim, a conta que temos que fazer já não tem mais vírgulas:
Então, há 320 milhas em 512 quilômetros.
Você também pode se interessar:
- Multiplicação de números decimais – Aprenda a multiplicar números com vírgula
- Atividades com números decimais
- Arredondamento e estimativa – Números inteiros e decimais

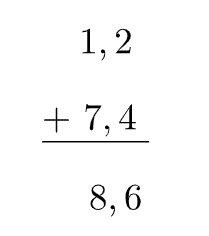
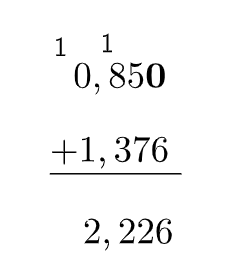
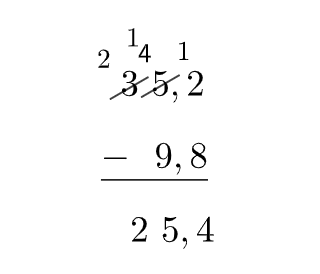

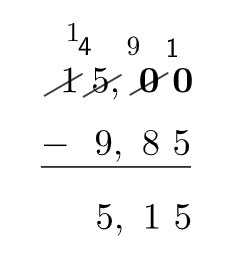
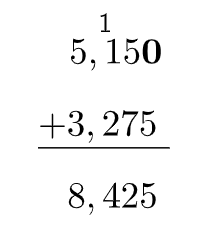
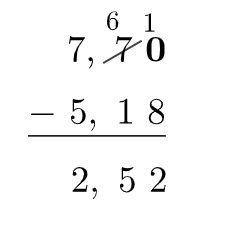

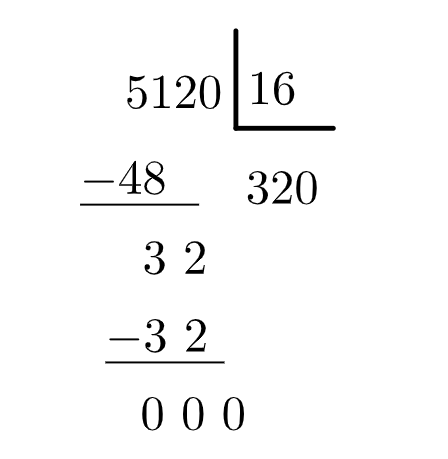
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.