Paralelepípedo
O paralelepípedo é uma figura geométrica tridimensional, um caso específico de prisma. Saiba como ele é formado, quais são os seus tipos e aprenda a calcular as áreas e o volume.
O que são paralelepípedos? Os paralelepípedos são sólidos geométricos estudados em Geometria Espacial.
Para ser chamado de paralelepípedo, um sólido geométrico tem que ser um prisma cujas bases e faces são paralelogramos, como quadrados, retângulos e losangos.
Um paralelepípedo é formado pelos seguintes elementos: faces, arestas e vértices.
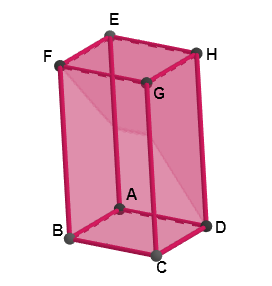
Faces, arestas e vértices do paralelepípedo
Em um paralelepípedo, temos:
- 6 faces (sendo 4 faces laterais e duas bases)
- 12 arestas
- 8 vértices
Faces
As faces são figuras geométricas planas com quatro lados, que ao se encontrarem formam o paralelepípedo. As faces laterais opostas têm o mesmo tamanho e as duas bases também.
Na imagem acima, o polígono é uma das faces do paralelepípedo.
Arestas
As arestas são os segmentos de reta que se formam no encontro de duas faces.
Por exemplo, os segmentos e
são arestas no paralelepípedo da figura.
Vértices
Os vértices são os pontos onde as arestas se encontram.
Na imagem, os pontos são os vértices.
Classificação do paralelepípedo
Os paralelepípedos podem ser classificados em retos ou oblíquos.
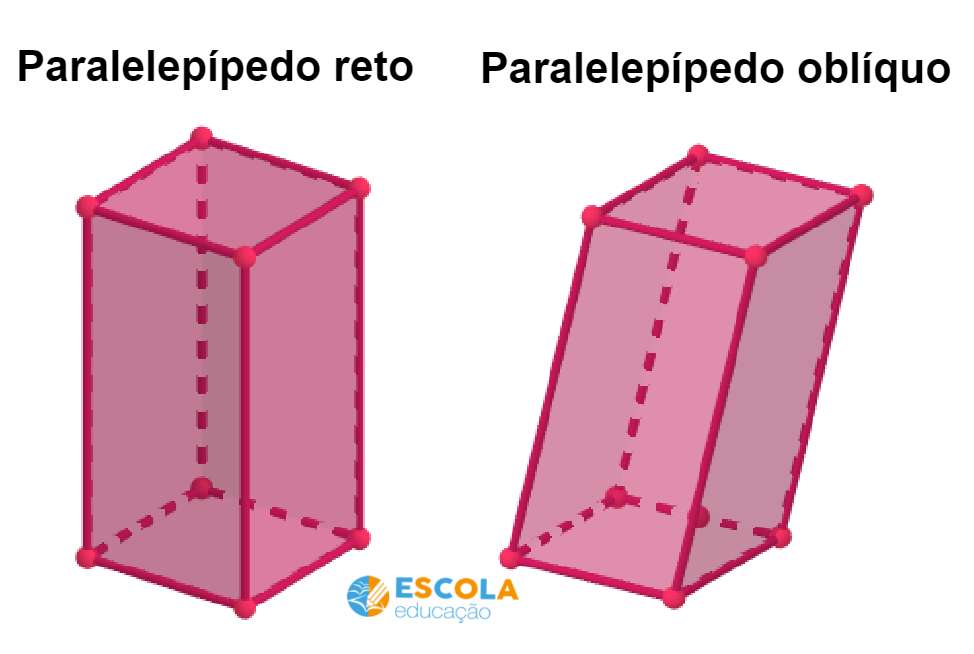
Paralelepípedo reto
Um paralelepípedo é reto (ou retângulo) quando suas arestas formam um ângulo reto (90º) com as bases. Quando um paralelepípedo reto possui todas as faces quadradas, ele é chamado de cubo.
Paralelepípedo oblíquo
Um paralelepípedo é oblíquo quando suas arestas não formam um ângulo reto (90º) com as bases.
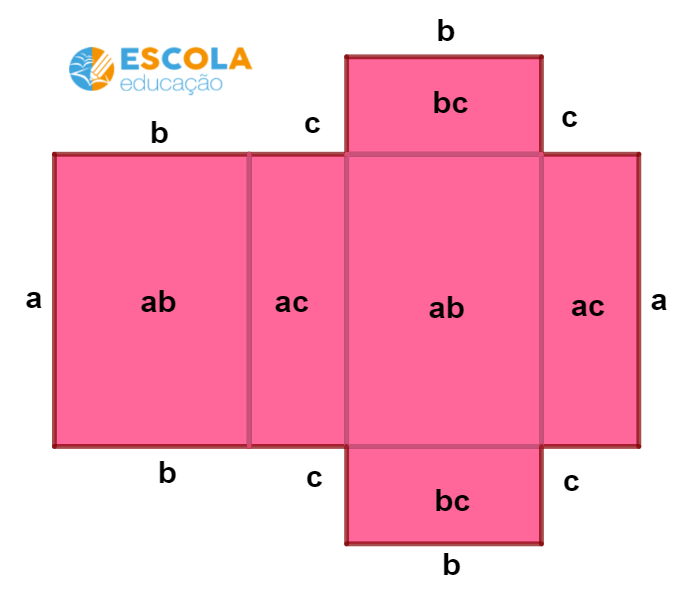
Planificação do paralelepípedo
A seguir, temos a planificação de um paralelepípedo de arestas , em que
é o comprimento,
é a largura e
é a altura.
Essa figura auxiliará no entendimento das fórmulas do paralelepípedo.
Fórmulas do paralelepípedo
Área da base
Considerando ab a base do paralelepípedo, a área da base () pode ser expressa como:
Área da lateral
Considerando as quatro faces laterais: ac, bc, ac e bc, a área da lateral () é dada por:
Área total
A área total () de um paralelepípedo é dada pela soma da área de todas as 6 faces, podendo ser expressa da seguinte forma:
Volume
O volume () de um paralelepípedo é dado pela multiplicação das medidas das arestas, isto é,
Diagonal
Considerando um paralelepípedo de arestas , em que
é o comprimento,
é a largura e
é a altura, temos que a diagonal (
) é dada por:
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.