Prisma – Figura geométrica
Os prismas são figuras geométricas espaciais. Veja quais são os elementos, as classificações e as fórmulas da área e do volume de um prisma.
Os prismas são figuras tridimensionais (possuem comprimento, largura e altura) e objetos de estudo da Geometria Espacial.
Em um prisma, as superfícies são compostas por uma quantidade finita de faces. Duas dessas faces são chamadas de bases, elas são polígonos congruentes e estão localizadas em planos paralelos distintos. As outras faces são chamadas de faces laterais.
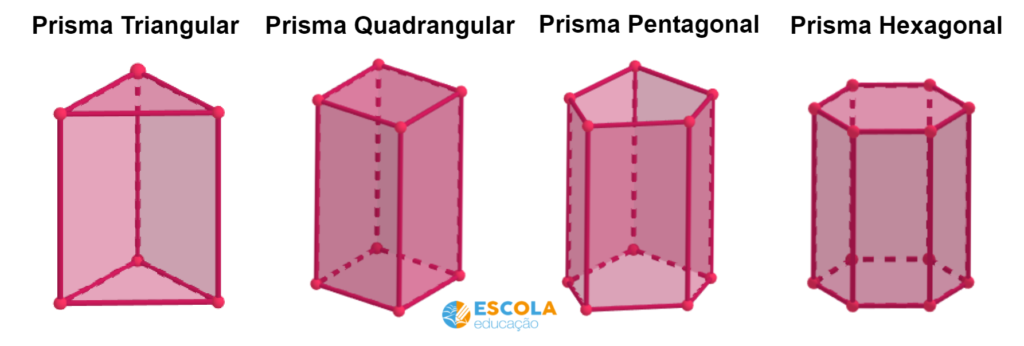
De acordo com o formato da base, os prismas recebem nomes específicos. Veja alguns exemplos:
- Prisma triangular: suas bases são triângulos;
- Prisma quadrangular: suas bases são quadrados;
- Prisma pentagonal: suas bases são pentágonos;
- Prisma hexagonal: suas bases são hexágonos.
Elementos do prisma
Um prisma é composto pelos seguintes elementos:
Faces: As faces de um prisma são os lados que o formam.
As duas faces paralelas e congruentes são as bases e as outras faces são as faces laterais.
Arestas: As arestas são os segmentos de reta que se formam no encontro de duas faces.
Vértices: Os vértices são os pontos de encontro entre as arestas.
Altura: A altura é a distância entre os planos das bases.
Classificação dos prismas
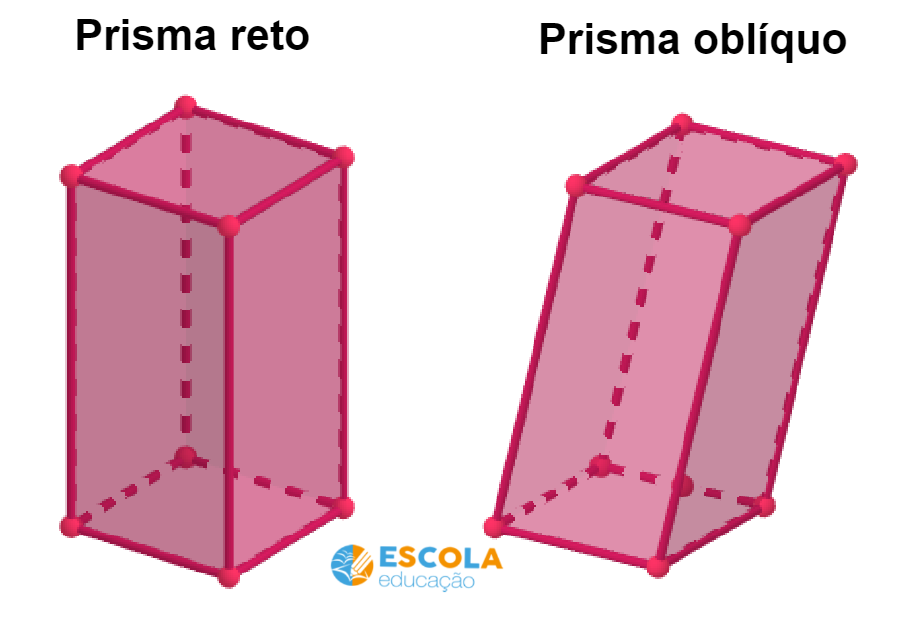
De acordo com a posição das arestas laterais e da base, os prismas podem ser classificados em retos ou oblíquos.
Prisma reto: Um prisma é reto quando as arestas laterais são perpendiculares a base, ou seja, formam ângulos de 90º.
Em prismas retos, as faces laterais serão sempre retangulares.
Prisma oblíquo: Um prisma é oblíquo quando as arestas laterais não são perpendiculares a base.
Fórmulas do prisma (Áreas do prisma – lateral e total)
Área lateral
A área lateral () de um prisma é a soma das áreas das faces laterais. Cada face lateral do prisma é um paralelogramo e sua área consiste na multiplicação da medida da aresta da base pela altura do prisma.
Assim, considerando o número de faces laterais em um prisma, a área lateral é dada por:
Em que:
é o número de faces laterais do prisma;
é a medida da aresta da base do prisma;
é a altura do prisma.
Área total
A área total () de um prisma é a soma da área lateral mais a área das bases (
). Assim, a área total de um prisma pode ser expressa da seguinte forma:
A área da base varia de acordo com o prisma. Por exemplo, se for um prisma triangular, a área da base é a área de um triângulo, se for um prisma quadrangular, é a área de um quadrado, e assim por diante.
Volume do prisma
O volume () de um prisma é dado pela multiplicação da área da base pela altura do prisma, isto é,
Veja também:


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.