Cone
O cone é um figura geométrica espacial que pode ser classificada em mais de um tipo. Veja quais os tipos de cones e aprenda a calcular a área total, a área da base, a área da lateral e o volume dessa figura.
O cone é uma figura geométrica espacial, que é formada por segmentos de reta que partem de um círculo até um ponto em comum.
O círculo possui um centro C e um raio r e, no cone, ele é chamado de base. Já o ponto em comum é chamado de vértice e se localiza em um plano diferente do plano onde está a base.
Além disso, em um cone, temos que:
- Qualquer segmento de reta que liga a circunferência do círculo ao vértice é denominado geratriz;
- A distância entre plano da base e o vértice é a altura do cone.
- A reta que passa pelo centro da base e o vértice é chamado de eixo.
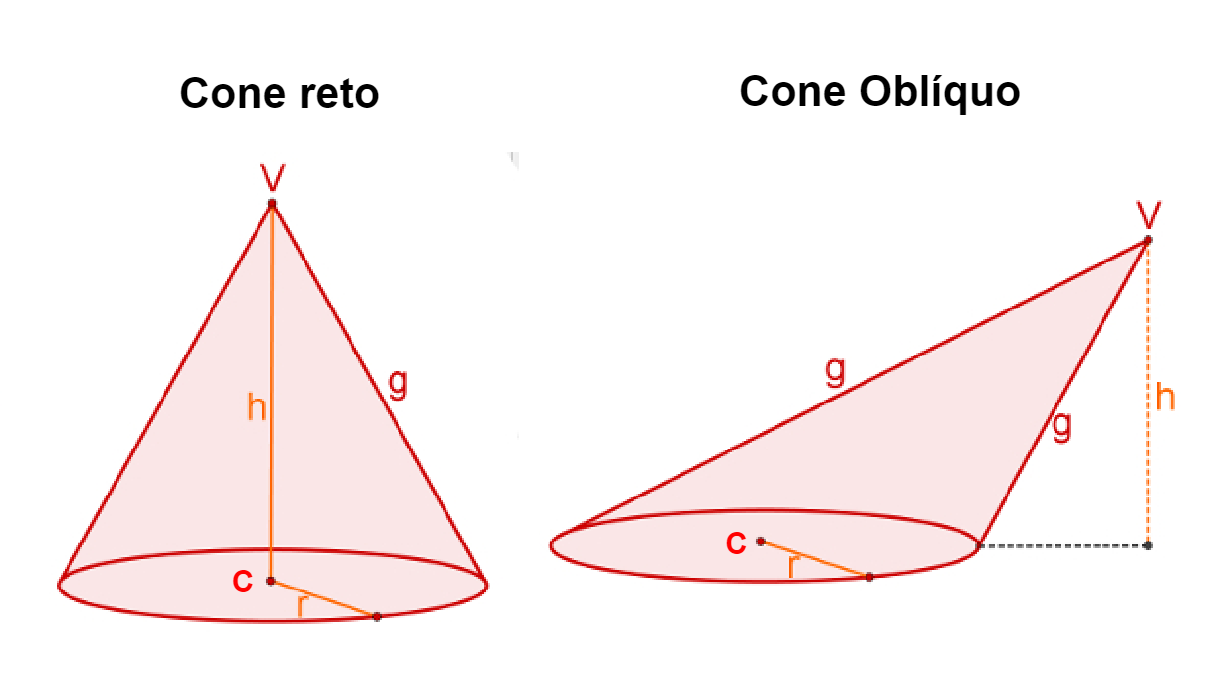
Veja a representação de um cone e seus elementos:
- V: vértice
- C: centro da base (círculo)
- r: raio da base (círculo)
- h: altura
- g: geratriz
Classificação dos cones
Um cone pode ser classificado em cone reto e em cone oblíquo.
Cone reto: Um cone é classificado como cone reto quando o eixo e o plano da base são perpendiculares, formando um ângulo reto, 90º. Nesse tipo de cone, o eixo é igual a altura.
Assim, em um cone reto, a altura (h), o raio (r) e a geratriz(g) são os três lados de um triângulo retângulo e essas três medidas podem ser relacionadas a partir do Teorema de Pitágoras, que nos permite dizer que , ou ainda, aplicando a raiz quadrada, que
.
Além disso, uma outra característica desse tipo de cone, é que todas as geratrizes são congruentes, ou seja, elas têm a mesma medida.
Cone oblíquo: Um cone é classificado como cone oblíquo quando o eixo e o plano da base não são perpendiculares.
Fórmulas do cone
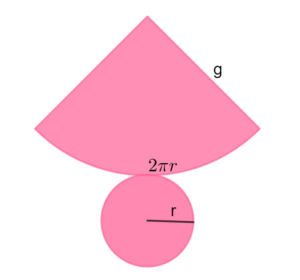
Na imagem abaixo, temos a planificação de um cone. A visualização do que seria um cone em um único plano, ou um “cone aberto”, facilitará no entendimento das fórmulas que veremos a seguir.
Área total (ou área externa)
A área total de um cone, ou área externa, é dada pela soma da área da base mais a área da lateral, isto é,
Área da base
A base de um cone é um círculo de raio r. Portanto, a área da base de um cone é igual a área de um círculo de raio r, ou seja:
O valor de é aproximadamente 3,14.
Área da lateral
A área da lateral de um cone é expressa da seguinte forma:
Explicação: A área da lateral de um cone é a área de um arco de comprimento (perímetro) igual a , que faz parte de um setor circular com raio g , área igual a
e perímetro
.
Então, chamando de a área da lateral, até então desconhecida, vamos utilizar uma regra de três simples para descobrir o valor dessa incógnita.
As informações que temos sobre o perímetro e a área do setor circular e o perímetro e a área da lateral podem ser organizadas em uma tabela:
| Perímetro | Área |
Assim, temos a seguinte proporção:
Logo, temos que a área da lateral é igual a , como queríamos mostrar.
Então, a área total ou área externa de um cone é dada por:
Volume do cone
Em um cone, o volume corresponde a 1/3 do multiplicação entre a área da base e a altura. Assim, a fórmula para calcular o volume do cone é:
Veja também: Circunferência – Definição, características e equação reduzida


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.