Plano cartesiano – O que é, como construir um, como fazer o produto cartesiano

Amantes ou não da matemática, em algum momento de nossa vida vida escolar, precisamos ou vamos precisar utilizar um plano cartesiano.

Então, o melhor é não perder tempo e aprender tudo o que precisamos sobre essa importante ferramenta da matemática.

O que é um plano cartesiano?

Na matemática, um plano cartesiano é um sistema, construído a partir de duas retas perpendiculares, para representar a posição de pontos.

Mas o que significa dizer que duas retas são perpendiculares? Significa que temos uma reta na horizontal e outra na vertical, e elas se cruzam em um determinado ponto, formando um ângulo de 90º.

Em um plano cartesiano, a reta na horizontal é chamada de eixo x ou eixo das abscissas e a reta na vertical é o eixo y ou eixo das ordenadas.

O plano cartesiano tem muitas aplicações, ele é uma ferramenta indispensável, por exemplo, na geometria, no estudo de funções e na cartografia, para fazer representações gráficas relacionadas a superfície terrestre.

Como fazer um plano cartesiano

Vamos começar pelo eixo x, ou eixo das abscissas.

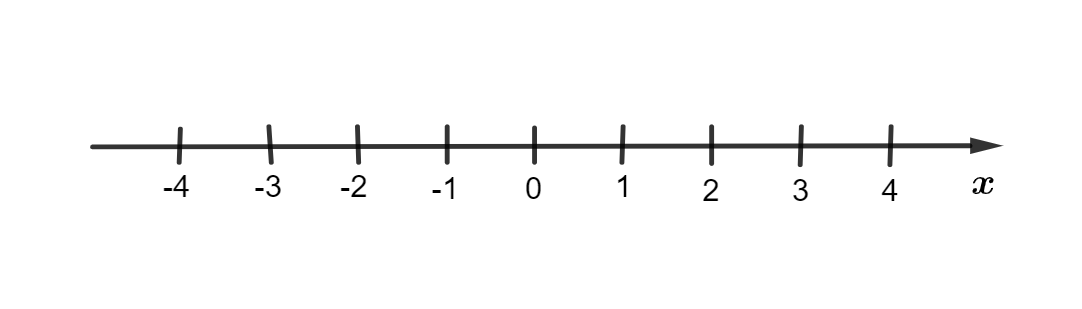
Primeiro, traçamos um reta na horizontal. Depois, marcamos os números inteiros, colocando a direita do zero os números positivos e a esquerda dele, os números negativos.

As retas são infinitas, então marcamos apenas uma parte dos números. Para exemplificar, escolhemos marcar de -4 até 4.
Agora, vamos fazer o eixo y, ou eixo das ordenadas.

Traçamos uma reta perpendicular ao eixo x, tal que o ponto de cruzamento entre as duas retas seja no par ordenado (0,0), também chamado de ponto de origem.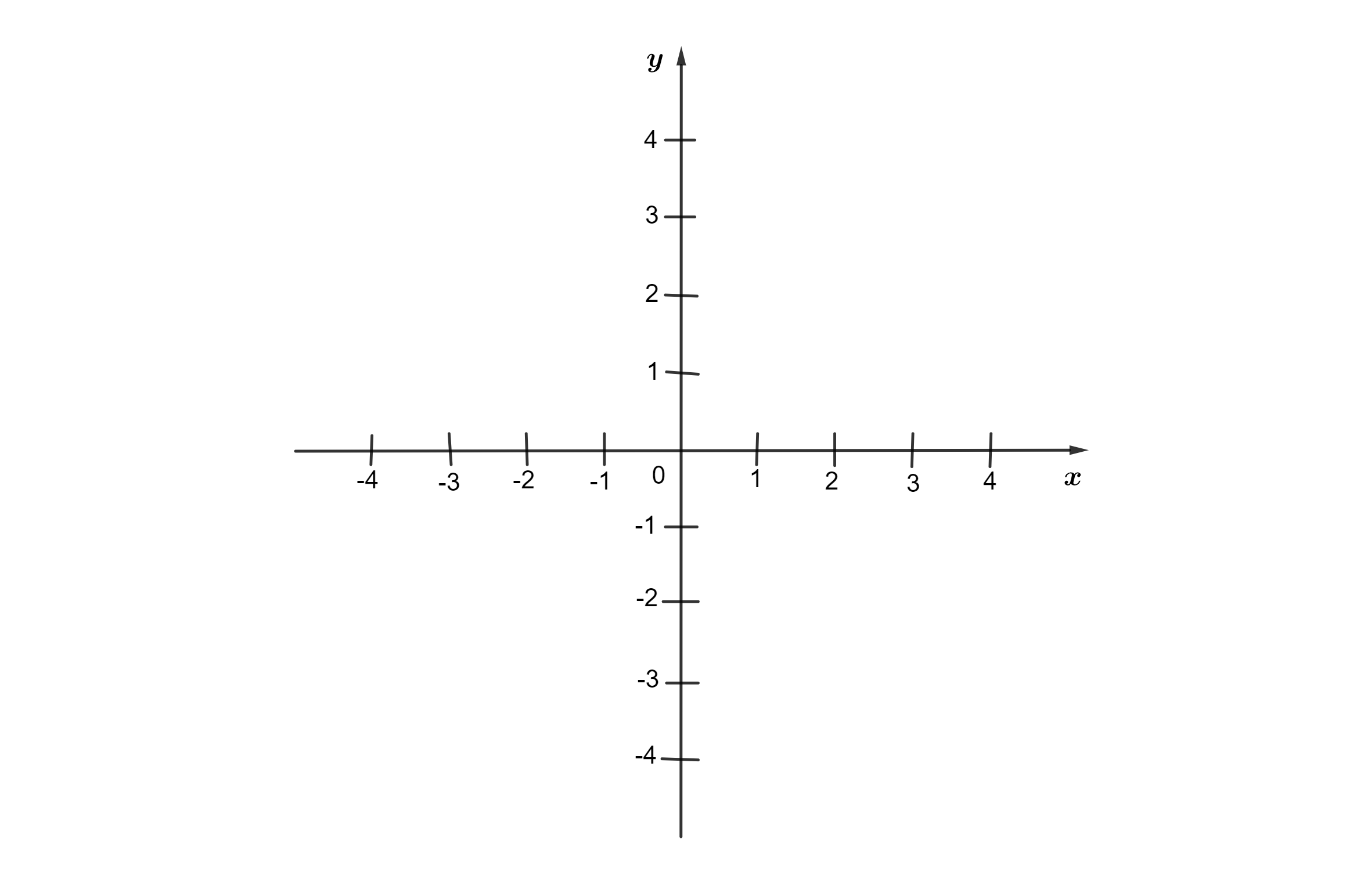O plano cartesiano está pronto. Mas como localizamos ou marcamos pontos nesse plano? Isso é o que vamos ver agora.

Exemplos – Como localizar pontos no plano cartesiano

Cada ponto no plano cartesiano será representado por um par ordenado do tipo (x, y).

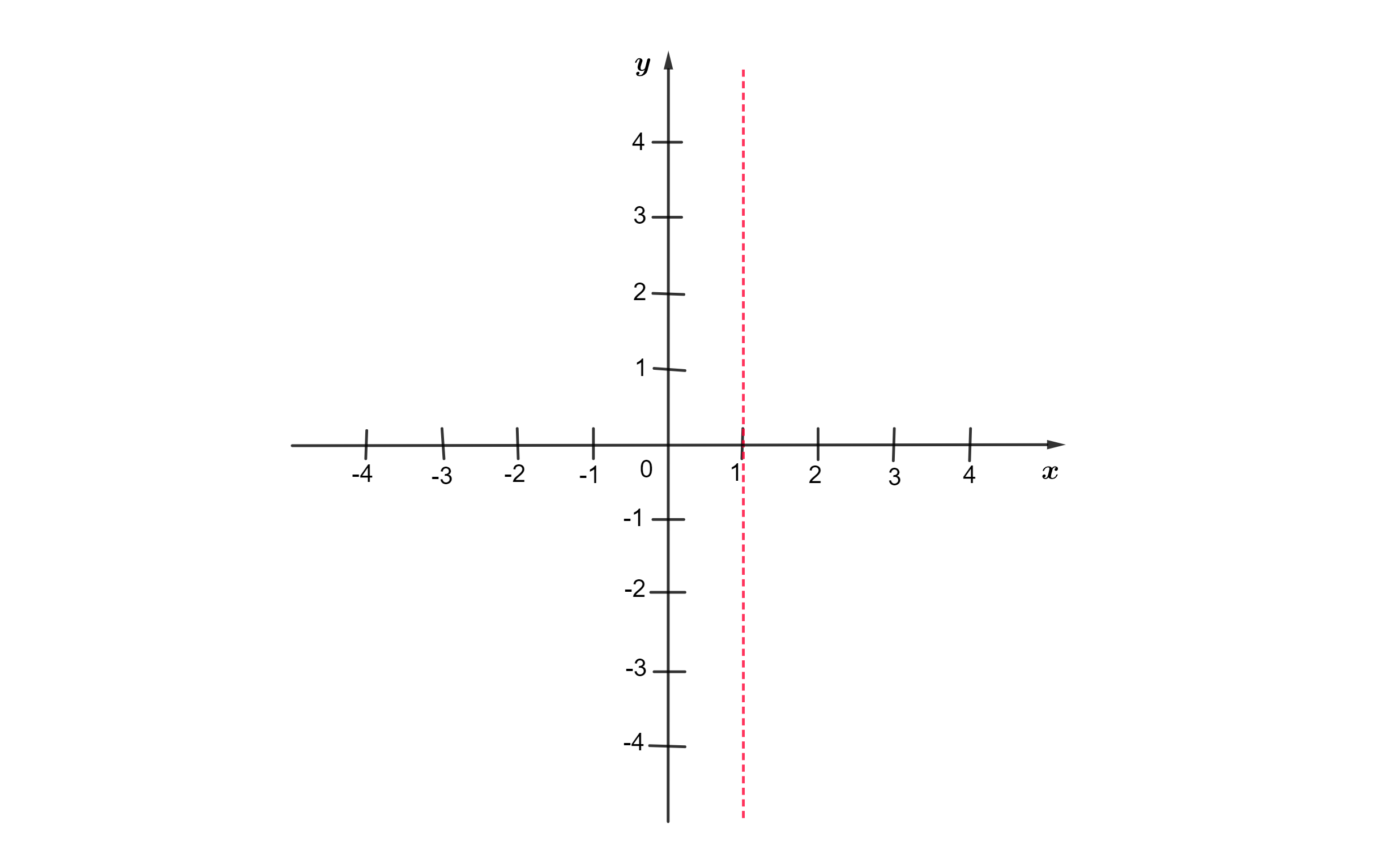
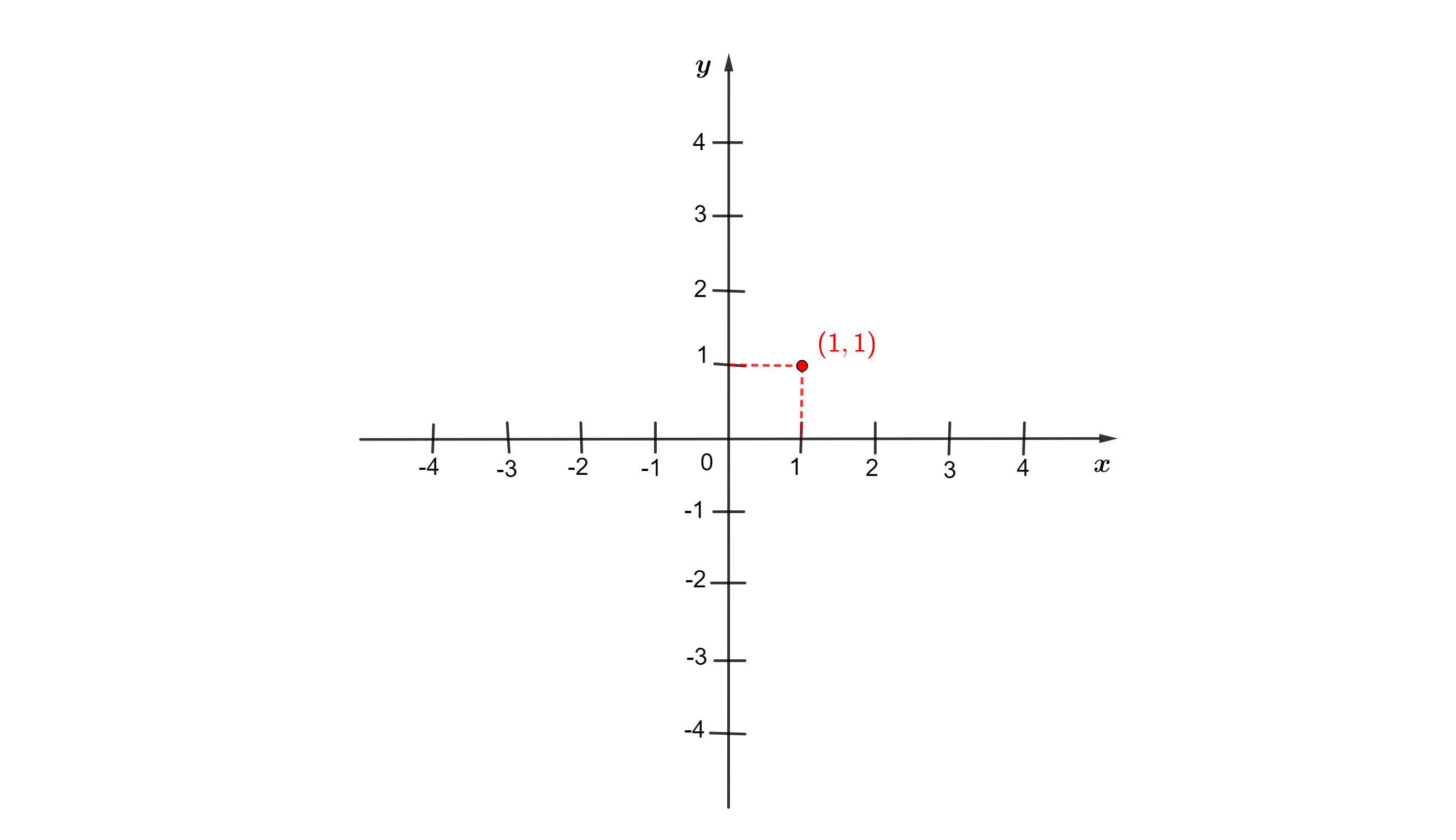
Exemplo 1. Vamos localizar o ponto (1,1) no plano:

Passo 1. Localizamos o valor de x no eixo das abscissas. Neste caso, x é igual a 1. Vamos traçar uma reta perpendicular ao eixo x, passando pelo ponto x = 1.
Passo 2. Localizamos o valor de y, que também é 1, no eixo das ordenadas. Traçamos uma reta perpendicular ao eixo y, passando pelo ponto y = 1.Observe que essas duas retas pontilhadas se cruzam em um ponto. Esse ponto de cruzamento é o ponto (1,1).

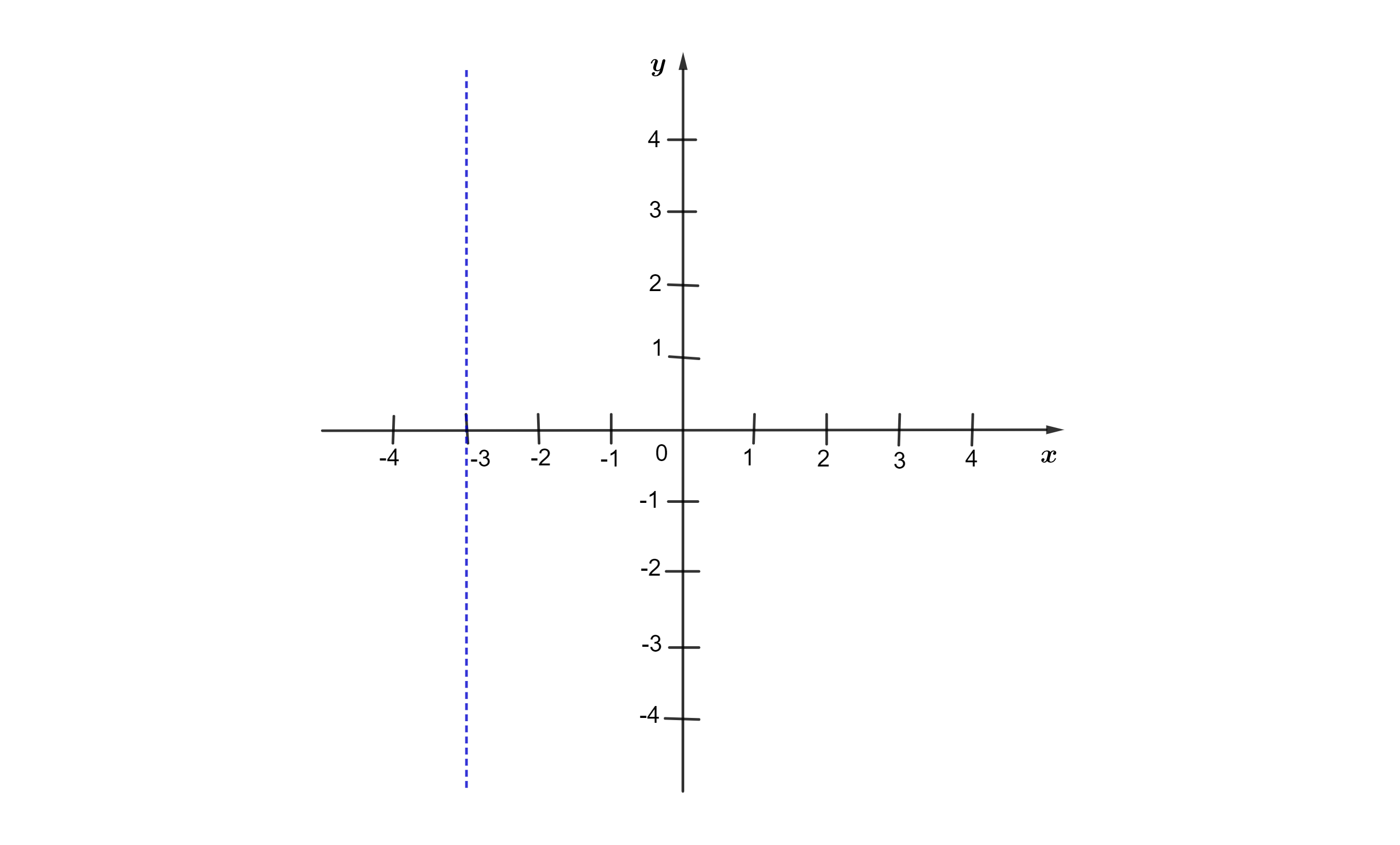
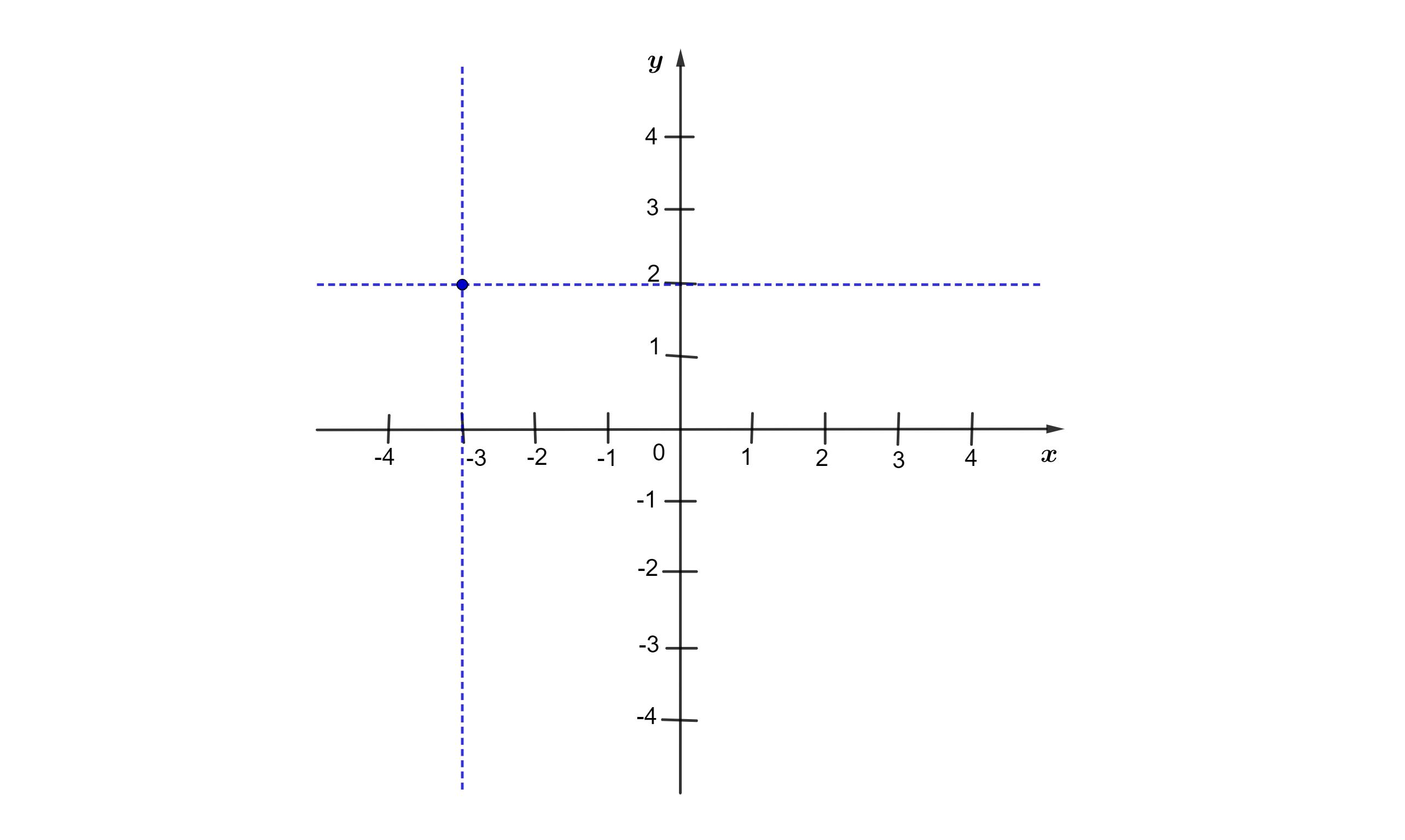
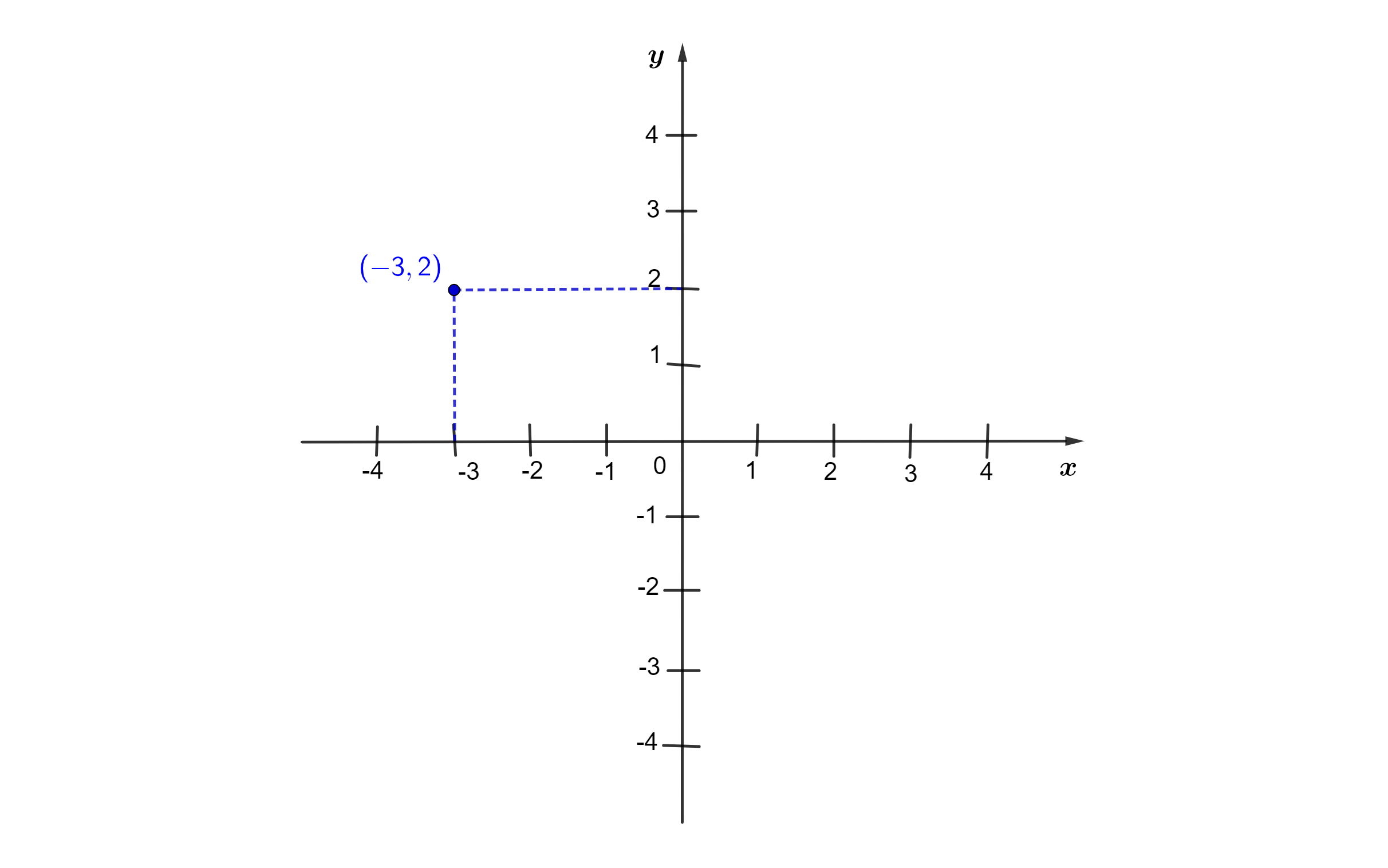
Exemplo 2. Vamos marcar o ponto (-3, 2) no plano:

Passo 1. Localizamos o valor de x no eixo das abscissas. Neste caso, x é igual a -3. Vamos traçar uma reta perpendicular ao eixo x, passando pelo ponto x = -3.
Passo 2. Localizamos o valor de y, que é 2, no eixo das ordenadas. Traçamos uma reta perpendicular ao eixo y, passando pelo ponto y = 2.
Novamente, temos um ponto de cruzamento. Esse ponto de cruzamento é o ponto (-3,2).

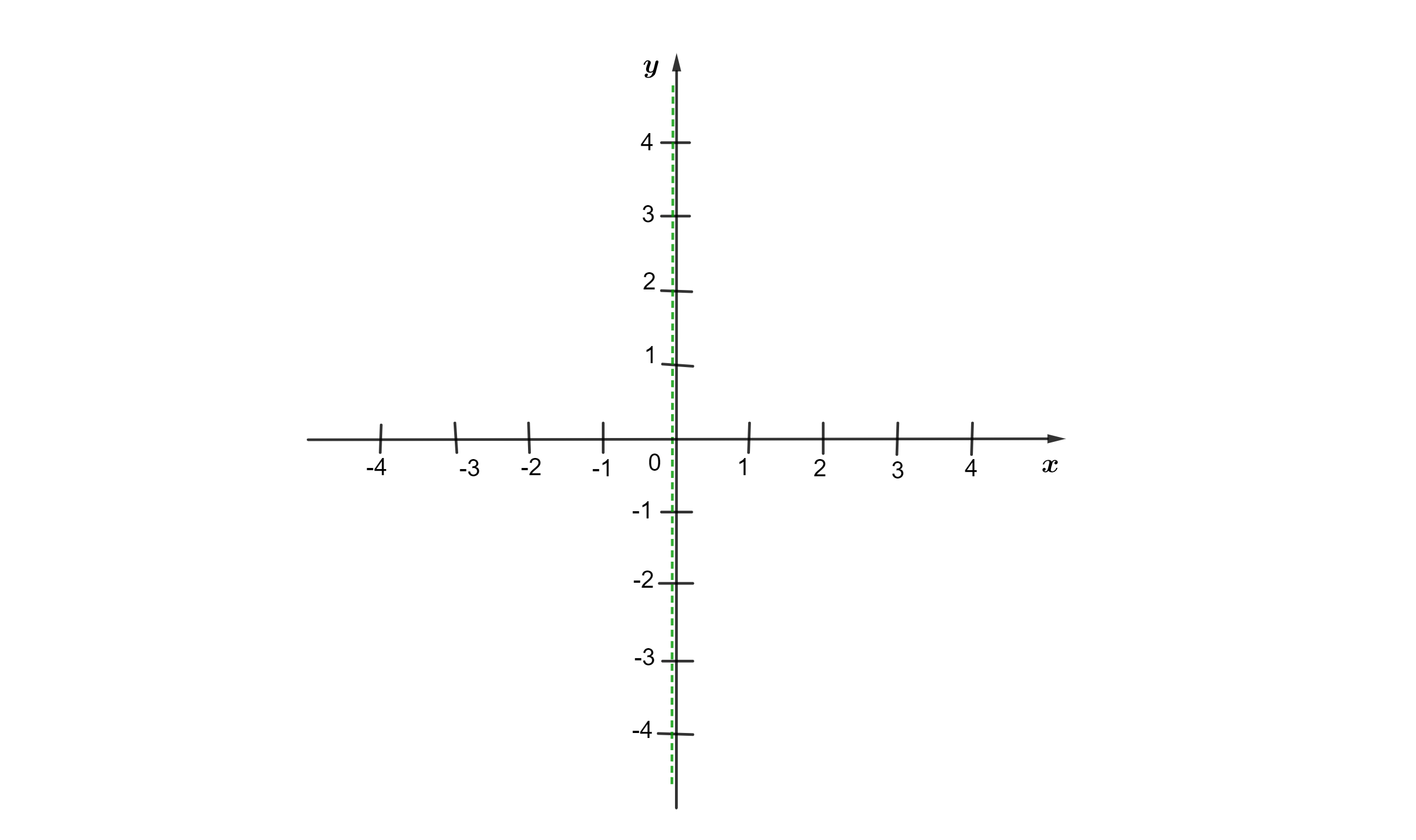
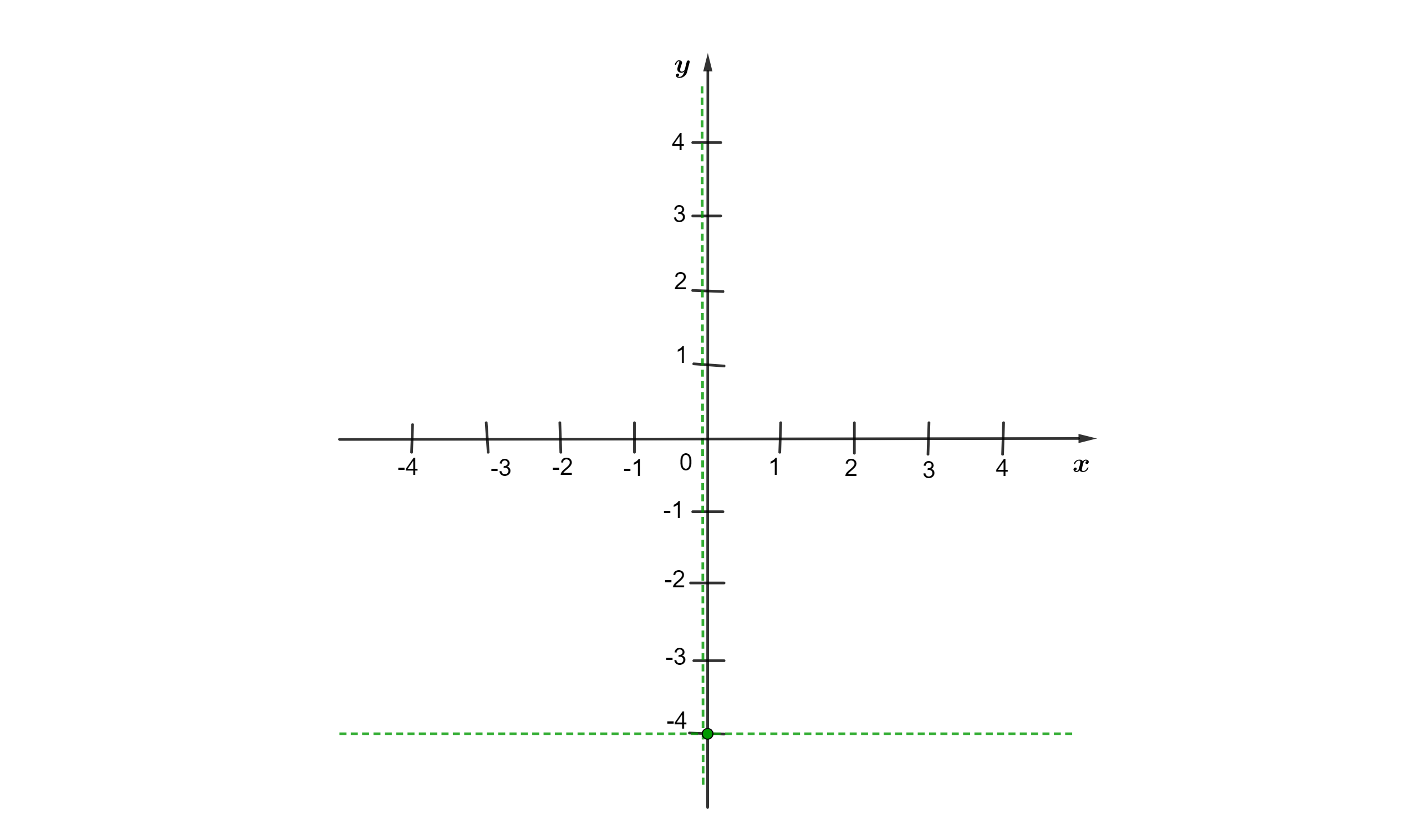
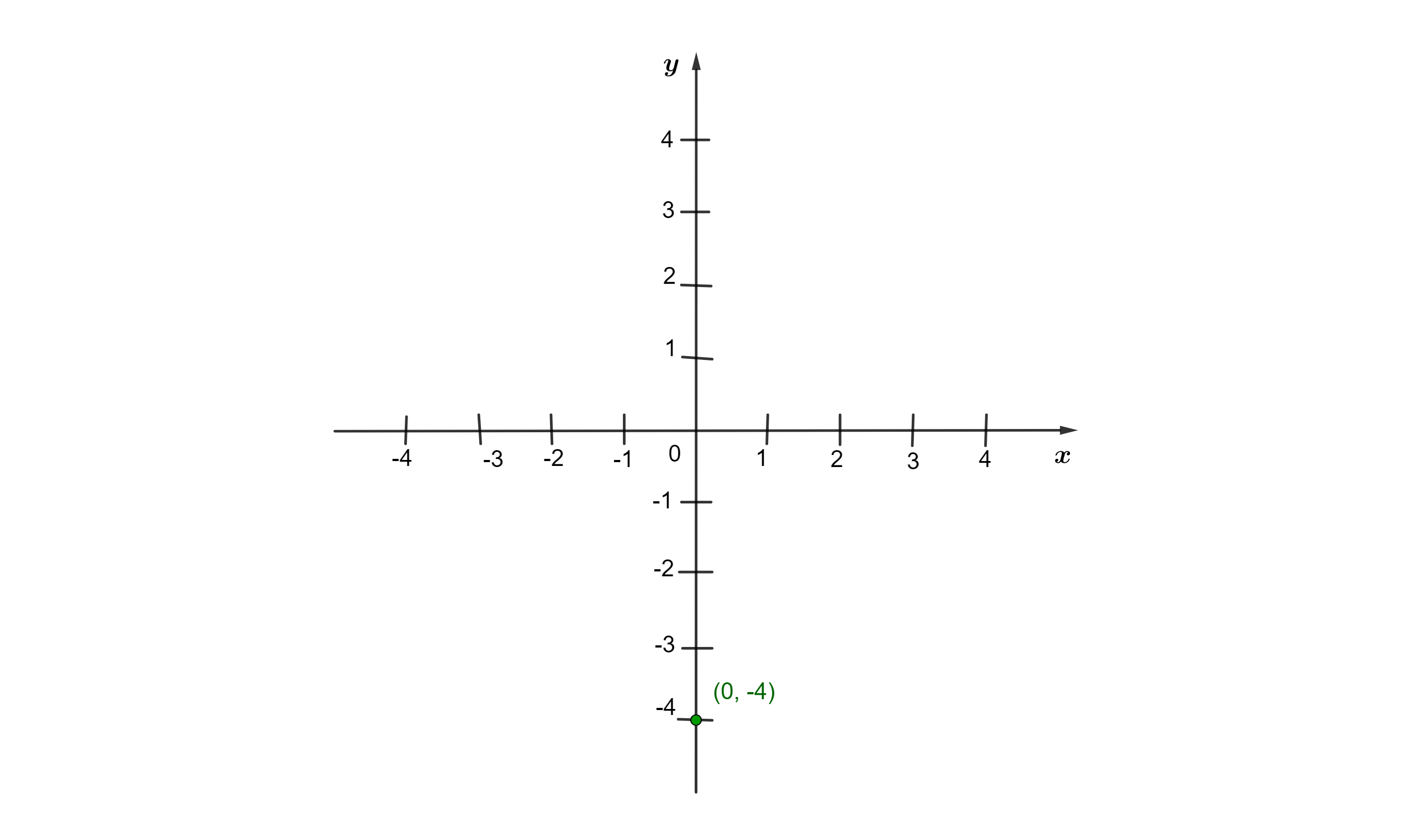
Exemplo 3. Vamos localizar o ponto (0,-4) no plano:

Passo 1. Localizamos o valor de x no eixo das abscissas. Neste caso, x é igual a 0. Vamos traçar uma reta perpendicular ao eixo x, passando pelo ponto x = 0. Veja que essa reta coincide com o eixo y.
Passo 2: Localizamos o valor de y, que é -4, no eixo das ordenadas. Traçamos uma reta perpendicular ao eixo y, passando pelo ponto y = -4.
O ponto de cruzamento é o ponto (0, -4).

Produto cartesiano

Considere dois conjuntos X e Y. O produto cartesiano dos conjuntos X e Y é formado por todos os pares ordenados (x,y) cujo primeiro termo pertence a X e o segundo pertence a Y.

Exemplo: Seja X = {1, 2, 3} e Y = {2, 3}, vamos fazer o produto entre X e Y, isto é, (X  Y):

• Formamos todos os pares ordenados possíveis fixando x = 1 e variando o valor de y  (1, 2), (1, 3)
• Formamos todos os pares ordenados possíveis fixando x = 2 e variando o valor de y  (2, 2), (2, 3)
• Formamos todos os pares ordenados possíveis fixando x = 3 e variando o valor de y  (3, 2), (3, 3)

Então, o conjunto formado pelo produto entre X e Y é:

X  Y = { (1, 2), (1, 3), (2, 2), (2, 3), (3, 2), (3, 3) }

Observação: X  Y é diferente de Y  X

O conjunto formado pelo produto entre Y e X é:

Y  X = { (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3) }

O ponto (1, 2) é diferente do ponto (2, 1).

Você também pode se interessar:

• Geometria plana
• Ângulos – Tipos, classificações e exemplos
• Circunferência – Definição, características e equação reduzida